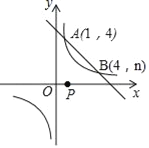
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
参考答案:
【答案】(1)y=![]() ;(2)y=﹣x+5;(3)(
;(2)y=﹣x+5;(3)(![]() ,0)
,0)
【解析】试题分析:(1)将点A(1,4)代入反比例函数解析式可得其解析式;
(2)先根据反比例函数解析式求得点B坐标,再由A、B坐标可得直线解析式;
(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,根据B的坐标求得B′的坐标,然后根据待定系数法求得直线AB′的解析式,进而求得与x轴的交点即可.
解:(1)把A(1,4)代入y=![]() ,得:m=4,
,得:m=4,
∴反比例函数的解析式为y=![]() ;
;
(2)把B(4,n)代入y=![]() ,得:n=1,
,得:n=1,
∴B(4,1),
把A(1,4)、(4,1)代入y=kx+b,得: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式为y=﹣x+5;
(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,
∵B(4,1),
∴B′(4,﹣1),
设直线AB′的解析式为y=mx+n,
∴![]() ,
,
解得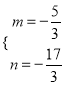 ,
,
∴直线AB′的解析式为y=﹣![]() x+
x+![]() ,
,
令y=0,得﹣![]() x+
x+![]() =0,
=0,
解得x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一楼房AB后有一假山,其坡度为i=1:
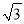 ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)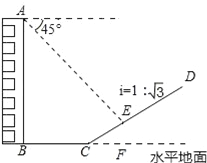
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△PAD是等边三角形,则∠BPC等于( )
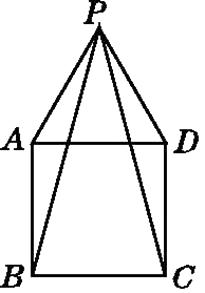
A.20°
B.30°
C.35°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】教室里,第6列第3个座位记作(6,3),则第3列第5个座位记作_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,
设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是( )

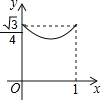
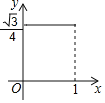
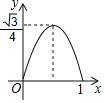
A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确结论的个数为( )
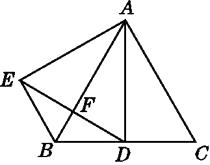
A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x(x+4)=﹣3(x+4)的解是 .
相关试题

