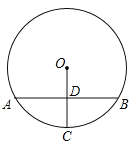
【题目】如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=( )
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
参考答案:
【答案】D
【解析】
利用垂径定理及已知可得到∠OAD=30°,再求出∠AOB的度数,再分情况讨论:当点P在优弧AB上时,利用圆周角定理就可取出∠P的度数;当点P在劣弧上时,利用圆内接四边形的对角互补,就可求出∠AP1B的度数.
连接OA,OB,
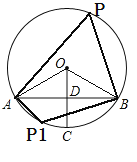
∵ 弦AB垂直平分半径OC
∴OD=![]() OA,
OA,
∴∠OAD=30°,
∵OA=OB
∴∠OAB=∠OBA=30°,
∴∠AOB=180°-∠OAB-∠OBA=180°-30°-30°=120°;
当点P在优弧AB上时
∠APB=![]() ∠AOB=
∠AOB=![]() ×120°=60°;
×120°=60°;
当点P在劣弧上时,
∠APB+∠AP1B=180°
∴∠AP1B=180°-60°=120°.
∴∠APB=120°或60°.
故答案为:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方形
 中,
中,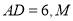 在
在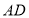 上从
上从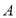 向
向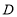 运动,连接
运动,连接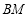 交
交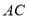 于
于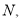 连接
连接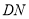 .
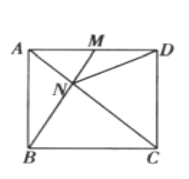
.
(1)证明:无论
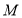 运动到
运动到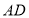 上的何处,都有
上的何处,都有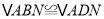 ;
;(2)当
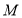 运动到何处时,
运动到何处时,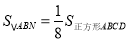 ?
?(3)若
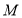 从
从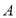 到
到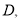 再从
再从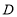 到
到 ,在整个运动过程中,
,在整个运动过程中,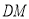 为多少时,
为多少时,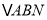 是等腰三角形?
是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c与x轴交于A、B两点,A(﹣5,0),与y轴交于C(0,﹣5),并且对称轴x=﹣3.
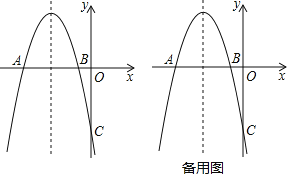
(1)求抛物线的解析式;
(2)P在x轴上方的抛物线上,过P的直线y=x+m与直线AC交于点M,与y轴交于点N,求PM+MN的最大值;
(3)点D为抛物线对称轴上一点,
①当△ACD是以AC为直角边的直角三角形时,求D点坐标;
②若△ACD是锐角三角形,求点D的纵坐标的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线M:y=-
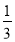 x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )
x2+2向左平移2个单位,再向上平移1个单位,得到抛物线M'.若抛物线M'与x轴交于A、B两点,M'的顶点记为C,则∠ACB=( )A.45°B.60°C.90°D.120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在三边互不相等的△ABC中, D,E,F分别是AB,AC,BC边的中点.连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有( )
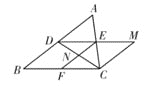
A.3对B.4对C.5对D.6对
-
科目: 来源: 题型:
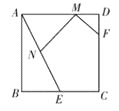
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:①
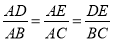 ;②
;② 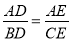 ;③
;③ 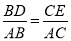 .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
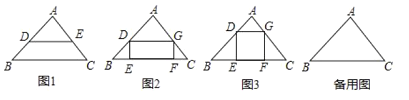
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
相关试题

