【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
参考答案:
【答案】
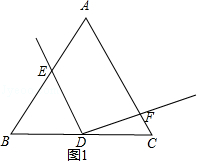
(1)
解:如图1所示:
(2)
解:想法1证明:如图2,过D作DG∥AB,交AC于G,
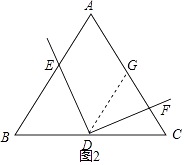
∵点D是BC边的中点,
∴DG= ![]() AB,
AB,
∴△CDG是等边三角形,
∴∠EDB+∠EDG=120°,
∵∠FDG+∠EDG=120°,
∴∠EDB=∠FDG,
∵BD=DG,∠B=∠FGD=60°,
∴△BDE≌△GDF,
∴DE=DF;
想法2证明:如图3,连接AD,
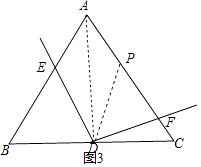
∵点D是BC边的中点,
∴AD是△ABC的对称轴,
作点E关于线段AD的对称点P,点P在边AC上,
∴△ADE≌△ADP,
∴DE=DP,∠AED=∠APD,
∵∠BAC+∠EDF=180°,
∴∠AED+∠AFD=180°,
∵∠APD+∠DPF=180°,
∴∠AFD=∠DPF,
∴DP=DF,
∴DE=DF;
想法3证明:如图4,连接AD,过D作DM⊥AB于M,DN⊥AC于N,

∵点D是BC边的中点,
∴AD平分∠BAC,
∵DM⊥AB于M,DN⊥AC于N,
∴DM=DN,
∵∠A=60°,
∴∠MDE+∠EDN=120°,
∵∠FDN+∠EDN=120°,
∴∠MDE=∠FDN,
∴Rt△MDE≌Rt△NDF,
∴DE=DF
(3)
解:当点F在AC边上时,BE+CF= ![]() AB,
AB,
当点F在AC延长线上时,BE﹣CF= ![]() AB,
AB,
证明:①当点F在AC边上时,如图5中,过点D作DM⊥AB于M,作DN⊥AC于N.

∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
在△BDM与△CDN中, 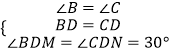 ,
,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE+CF=BM+EM+NC﹣FN=2BM=BD= ![]() AB;
AB;
②当点F在AC延长线上时,如图6,
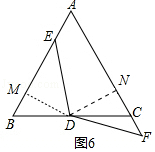
∵∠B=∠C=60°,BD=DC,∠BDM=∠CDN=30°,
∴△BDM≌△CDN,
∴BM=CN,DM=DN,
又∵∠EDF=120°=∠MDN,
∴∠EDM=∠NDF,
又∵∠EMD=∠FND=90°,
∴△EDM≌△FDN,
∴ME=NF,
∴BE﹣CF=BM+EM﹣(FN﹣CN)=2BM=BD= ![]() AB,
AB,
综上所述:当点F在AC边上时,BE+CF= ![]() AB;
AB;
当点F在AC延长线上时,BE﹣CF= ![]() AB.
AB.
【解析】(1)根据题目中的要求作图即可;(2)想法1,由已知得到△CDG是等边三角形,证得∠EDB=∠FDG,根据全等三角形的性质即可得到结论;想法2,如图3,连接AD,作点E关于线段AD的对称点P,点P在边AC上,根据全等三角形的性质得到DE=DP,∠AED=∠APD,等量代换得到∠AFD=∠DPF,于是得到结论;想法3,如图4,连接AD,过D作DM⊥AB于M,DN⊥AC于N,根据角平分线的性质得到DM=DN,根据全等三角形的性质即可得到结论;(3)当点F在AC边上时,过点D作DM⊥AB于M,作DN⊥AC于N.只要证明△BDM≌△CDN,△EDM≌△FDN即可解决问题,当点F在AC延长线上时,证明方法类似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数

100
150
200
500
800
1000
摸到白球的次数

58
96
116
295
484
601
摸到白球的频率

0.58
0.64
0.58
0.59
0.605
0.601
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场第一次用10000元购进甲、乙两种商品,销售完成后共获利2200元,其中甲种商品每件进价60元,售价70元;乙种商品每件进价50元,售价65元.
(1)求该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,且购进甲、乙商品的数量分别与第一次相同,甲种商品按原售价出售,而乙种商品降价销售,要使第二次购进的两种商品全部售出后,获利不少于1800元,乙种商品最多可以降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣3x+3与x轴、y轴分别父于A、B两点,点A关于直线x=﹣1的对称点为点C.

(1)求点C的坐标;
(2)若抛物线y=mx2+nx﹣3m(m≠0)经过A、B、C三点,求抛物线的表达式;
(3)若抛物线y=ax2+bx+3(a≠0)经过A,B两点,且顶点在第二象限.抛物线与线段AC有两个公共点,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点Q为坐标系上任意一点,某图形上的所有点在∠Q的内部(含角的边),这时我们把∠Q的最小角叫做该图形的视角.如图1,矩形ABCD,作射线OA,OB,则称∠AOB为矩形ABCD的视角.

(1)如图1,矩形ABCD,A(﹣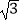 ,1),B(
,1),B( 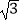 ,1),C(
,1),C( 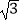 ,3),D(﹣
,3),D(﹣ 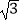 ,3),直接写出视角∠AOB的度数;
,3),直接写出视角∠AOB的度数; 
(2)在(1)的条件下,在射线CB上有一点Q,使得矩形ABCD的视角∠AQB=60°,求点Q的坐标;
(3)如图2,⊙P的半径为1,点P(1,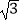 ),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围.
),点Q在x轴上,且⊙P的视角∠EQF的度数大于60°,若Q(a,0),求a的取值范围. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.我市区机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题:

(1)A组的频数是 ,本次调查样本的容量是 ;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC与△A′B′C′中,有下列条件:(1)
 ,(2)
,(2)  ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
相关试题

