【题目】某商场第一次用10000元购进甲、乙两种商品,销售完成后共获利2200元,其中甲种商品每件进价60元,售价70元;乙种商品每件进价50元,售价65元.
(1)求该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,且购进甲、乙商品的数量分别与第一次相同,甲种商品按原售价出售,而乙种商品降价销售,要使第二次购进的两种商品全部售出后,获利不少于1800元,乙种商品最多可以降价多少元?
参考答案:
【答案】(1)甲、乙两种商品分别是100件、80件;(2)5元
【解析】
试题分析:(1)设商场购进甲x件,乙购进y件.则根据“用10000元购进甲、乙两种商品、销售完成后共获利2200元”列出方程组;
(2)设乙种商品降价z元,则由“要使第二次购进的两种商品全部售出后,获利不少于1800元”列出不等式.
解:(1)设商场购进甲x件,乙购进y件.则
![]() ,
,
解得![]() .
.
答:该商场购进甲、乙两种商品分别是100件、80件;
(3)设乙种商品降价z元,则
10×100+(15﹣z)×80≥1800,
解得 z≤5.
答:乙种商品最多可以降价5元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣
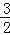 ,0),且与反比例函数y=
,0),且与反比例函数y=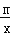 (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.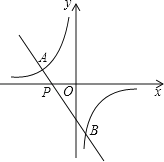
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a﹣b=0;②a+b+c>0;③c=﹣3a;④只有当a=
 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.其中正确的结论是 .(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】等式(x+6)0=1成立的条件是( )
A. x为有理数 B. x≠0 C. x≠6 D. x≠﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数为( )
①同位角相等;
②从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
③平面内经过一点有且只有一条直线与已知直线平行;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(2,5)与点Q关于x轴对称,则点Q的坐标是( )
A.(﹣2,5)
B.(2,﹣5)
C.(﹣2,﹣5)
D.(5,2)
相关试题

