【题目】题目:某校七年级学生乘车去参加社会实践活动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租这种客车的辆数:
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明列出不完整的方程为![]()
小红列出不完整的方程为![]()
(说明:其中“![]() ”表示运算符号,“
”表示运算符号,“![]() ”表示数字):
”表示数字):
(1)小明所列方程中![]() 表示的意义是________________________;
表示的意义是________________________;
小红所列方程中![]() 表示的意义是___________________________;
表示的意义是___________________________;
(2)选择两位同学的其中一位学生的做法,将其补充完整,并完整地解答这道题.
参考答案:
【答案】解:(1)客车的数量,学生的总人数;(2)见解析.
【解析】
(1)小明所列方程中的等量关系:总的人数不变.小红所列方程中的等量关系:客车数量不变.
(2)利用相应的等量关系列出方程并解答.
解:(1)根据总人数列方程,应是50x+12=55x-8,其中x表示该校租的客车数量.
根据客车数列方程,应该为:![]() ,其中y表示该校有y名学生去参加社会实践话动.
,其中y表示该校有y名学生去参加社会实践话动.
故答案是:该校租的客车数量.该校有y名学生去参加社会实践话动;
(2)小明:50x+12=55x-8
解方程得:x=4.
小红:![]() ,
,
解方程得:y=212,
![]() .
.
答:该校租了4辆客车,七年级学生212人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
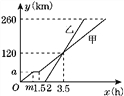
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 , B1C1交AC于点D,如果AD=2
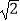 ,则△ABC的周长等于 .
,则△ABC的周长等于 . 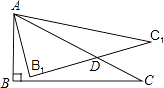
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
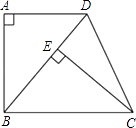
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据: ≈1.414,
≈1.414,  ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在解方程组
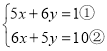 时,我们可以先①+②,得
时,我们可以先①+②,得 再②-①,得
再②-①,得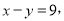 最后重新组成方程组
最后重新组成方程组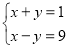 ,这种解二元一次方程组的解法我们称为二元一次方程组的轮换对称解法.
,这种解二元一次方程组的解法我们称为二元一次方程组的轮换对称解法.(1)用轮换对称解法解方程组
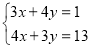 ,得_____________________________;
,得_____________________________;(2)如图,小强和小红一起搭积木,小强所搭的“小塔”高度为32cm,小红所搭的“小树”高度为3lcm,设每块A型积木的高为
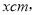 每块B型积木的高为
每块B型积木的高为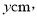 求
求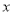 与
与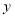 的值.
的值.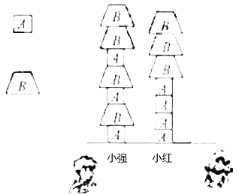
相关试题

