【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 , B1C1交AC于点D,如果AD=2 ![]() ,则△ABC的周长等于 .
,则△ABC的周长等于 . 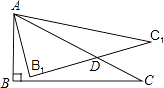
参考答案:
【答案】6+2 ![]()
【解析】解:在Rt△ABC中,∠ABC=90°,∠ACB=30°, 则∠BAC=60°,
将△ABC绕点A按逆时针方向旋转15°后,∠B1AD=45°,
而∠AB1D=90°,故△AB1D是等腰直角三角形,
如果AD=2 ![]() ,则根据勾股定理得,
,则根据勾股定理得,
AB1=2那么AB=AB1=2,
AC=2AB=4,
BC=2 ![]() ,
,
△ABC的周长为:AB+BC+AC=2+4+2 ![]() =6+2
=6+2 ![]() .
.
故本题答案为:6+2 ![]() .
.
【考点精析】通过灵活运用解直角三角形和旋转的性质,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,三个半圆依次相外切,它们的圆心都在x轴的正半轴上并与直线y=
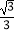 x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
x相切,设半圆C1、半圆C2、半圆C3的半径分别是r1、r2、r3 , 则当r1=1时,r3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
(1)如图1,∠BME,∠E,∠END的数量关系为 (直接写出答案);
(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数(用用含m的式子表示)
(3)如图3,点G为CD上一点,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
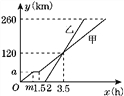
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1:y=kx+b与直线l2:y=bx+k在同一坐标系中的大致位置是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】题目:某校七年级学生乘车去参加社会实践活动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租这种客车的辆数:
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明列出不完整的方程为
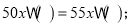
小红列出不完整的方程为
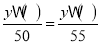
(说明:其中“
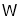 ”表示运算符号,“
”表示运算符号,“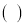 ”表示数字):
”表示数字):(1)小明所列方程中
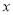 表示的意义是________________________;
表示的意义是________________________;小红所列方程中
 表示的意义是___________________________;
表示的意义是___________________________;(2)选择两位同学的其中一位学生的做法,将其补充完整,并完整地解答这道题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
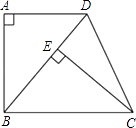
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
相关试题

