【题目】定义:在解方程组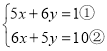 时,我们可以先①+②,得
时,我们可以先①+②,得![]() 再②-①,得
再②-①,得![]() 最后重新组成方程组
最后重新组成方程组![]() ,这种解二元一次方程组的解法我们称为二元一次方程组的轮换对称解法.
,这种解二元一次方程组的解法我们称为二元一次方程组的轮换对称解法.
(1)用轮换对称解法解方程组![]() ,得_____________________________;
,得_____________________________;
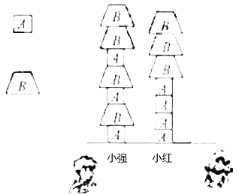
(2)如图,小强和小红一起搭积木,小强所搭的“小塔”高度为32cm,小红所搭的“小树”高度为3lcm,设每块A型积木的高为![]() 每块B型积木的高为
每块B型积木的高为![]() 求
求![]() 与
与![]() 的值.
的值.
参考答案:
【答案】解:(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据轮换对称解法的定义求解即可;
(2)根据小强所搭的“小塔”高度为32cm,小红所搭的“小树”高度为3lcm,列方程组求解即可.
解:(1)①+②,得
x+y=2,
②-①,得
x-y=12,
∴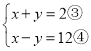 ;
;
③+④,得
2x=14,
x=7,
③-④,得
2y=-10,
y=-5,
∴![]() ;
;
(2)有题意得,
![]() ,
,
解得![]() ,
,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】题目:某校七年级学生乘车去参加社会实践活动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租这种客车的辆数:
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明列出不完整的方程为
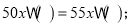
小红列出不完整的方程为
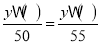
(说明:其中“
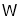 ”表示运算符号,“
”表示运算符号,“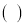 ”表示数字):
”表示数字):(1)小明所列方程中
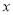 表示的意义是________________________;
表示的意义是________________________;小红所列方程中
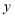 表示的意义是___________________________;
表示的意义是___________________________;(2)选择两位同学的其中一位学生的做法,将其补充完整,并完整地解答这道题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据: ≈1.414,
≈1.414,  ≈1.732)
≈1.732) -
科目: 来源: 题型:
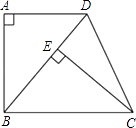
查看答案和解析>>【题目】小明同学三次到某超市购买A、B两种商品,其中仅有一次是由折扣的,购买数量及消费金额如下表:
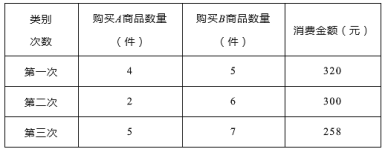
解答下列问题:
(1)第_______次购买的商品有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,则折扣数为______折;
(4)小明同学再次购买A、B两种商品共10件,在(3)的折扣数的前提下,这10件商品的消费金额不超过200元,求至少购买A商品的件数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题:
(1)参加调查的人数共有 人;
(2)将条形图补充完整;
(3)求在扇形图中表示“其它球类”的扇形的圆心角的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
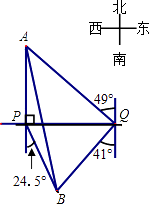
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)
相关试题

