【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
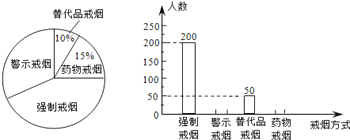
参考答案:
【答案】(1)500人.(2)补图见解析;(3)3500人。(4)5040人.
【解析】试题分析:(1)根据替代品戒烟50人占总体的10%,即可求得总人数;
(2)根据求得的总人数,结合扇形统计图可以求得药物戒烟的人数,从而求得警示戒烟的人数,再根据各部分的人数除以总人数,即可求得各部分所占的百分比;
(3)根据图中“强制戒烟”的百分比再进一步根据样本估计总体.
(4)第一期宣传后支持“警示戒烟”的市民约有3500×(1+增长率),第二期宣传后支持“警示戒烟”的市民约有3500×(1+增长率)(1+增长率).
试题解析:(1)50÷10%=500(人).
故一共调查了500人.
(2)由(1)可知,总人数是500人.
药物戒烟:500×15%=75(人);
警示戒烟:500-200-50-75=175(人);175÷500=35%;
强制戒烟:200÷500=40%.
完整的统计图如图所示:
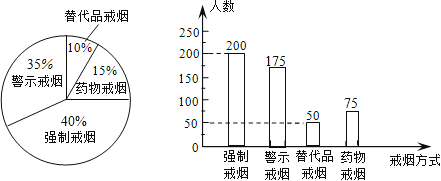
(3)10000×35%=3500(人),
答:大约有3500人支持“警示戒烟”这种方式;
(4)3500×(1+20%)2=5040(人),
答:两期宣传后支持“警示戒烟”的市民约有5040人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图16,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=

 +k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.
+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用公式法解﹣x2+3x=1时,先求出a、b、c的值,则a、b、c依次为( )
A.﹣1,3,1B.1,3,1C.﹣1,3,﹣1D.1,﹣3,﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2先向右平移2个单位,再向下平移3个单位,那么所得到抛物线的函数关系式是( )
A.y=(x﹣2)2﹣3
B.y=(x+2)2﹣3
C.y=(x﹣2)2+3
D.y=(x+2)2+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年国庆节放假八天,高速公路免费通行,各地风景区游人如织.其中闻名于世的北京故宫在10月1日的游客人数就已经达到了7万人,接下来的七天中,每天的游客人数变化(单位:万人)如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):

(1)10月3日的人数为万人;
(2)这八天,游客人数最多的是10月日,达到万人;游客人数最少的是10月日,为万人;
(3)这8天参观故宫的总人数约为万人(结果精确到万位)
(4)如果你们一家人打算在下一个国庆节参观故宫,请你对你们的出行日期提一个建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(1)这个用户12月用水量10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费元. -
科目: 来源: 题型:
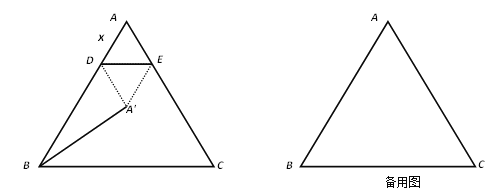
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x,△ADE的边DE上的高为y.
(1) 求出y与x的函数关系式;
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;
(3) 当x取何值时,△A' DB是直角三角形.
相关试题

