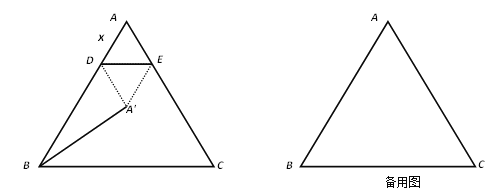
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D为AB边上的一动点(D不与A、B重合),过D作DE∥BC,交AC于点E.把△ADE沿直线DE折叠,点A落在点A'处.连结BA',设AD=x,△ADE的边DE上的高为y.
(1) 求出y与x的函数关系式;
(2) 若以点A'、B、D为顶点的三角形与△ABC 相似,求x的值;
(3) 当x取何值时,△A' DB是直角三角形.
参考答案:
【答案】(1)y=![]() (0<x<5).(2)x=
(0<x<5).(2)x=![]() .(3)当x=
.(3)当x=![]() 、x=
、x=![]() 时,△A'DB是直角三角形.
时,△A'DB是直角三角形.
【解析】试题分析:(1)先过A点作AM⊥BC,得出BM=![]() BC=3,再根据DE∥BC,得出AN⊥DE,即y=AN,再在Rt△ABM中,求出AM的值,再根据DE∥BC,求出△ADE∽△ABC,即可求出y与x的函数关系式;
BC=3,再根据DE∥BC,得出AN⊥DE,即y=AN,再在Rt△ABM中,求出AM的值,再根据DE∥BC,求出△ADE∽△ABC,即可求出y与x的函数关系式;
(2)根据△A'DE由△ADE折叠得到,得出AD=A'D,AE=A'E,再由(1)可得△ADE是等腰三角形,得出AD=A'D,AE=A'E,即可证出四边形ADA'E是菱形,得出∠BDA'=∠BAC,再根据∠BAC≠∠ABC,∠BAC≠∠C,得出∠BDA'≠∠ABC,∠BDA'≠∠C,从而证出△BDA'∽△BAC,即可求出x的值;
(3)先分三种情况进行讨论;第一种情况当∠BDA′=90°,得出∠BDA'≠90°;第二种情况当∠BA'D=90°,根据∠BAM<90°,∠BA'D<∠BAM,可得∠BA'D≠90°;第三种情况当∠A'BD=90°,根据∠A'BD=90°,∠AMB=90°,得出△BA'M∽△ABM,即可求出BA′的值,再在Rt△DBA'中,根据DB2+A'B2=A'D2,求出x的值,即可证出△A′DB是直角三角形;
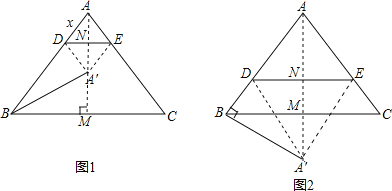
试题解析:(1)如图1,过A点作AM⊥BC,垂足为M,交DE于N点,则BM=![]() BC=3,
BC=3,
∵DE∥BC,
∴AN⊥DE,即y=AN.
在Rt△ABM中,AM=![]() =4,
=4,
∵DE∥BC,
∴△ADE∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴y=![]() (0<x<5).
(0<x<5).
(2)∵△A'DE由△ADE折叠得到,
∴AD=A'D,AE=A'E,
∵由(1)可得△ADE是等腰三角形,
∴AD=AE,
∴A'D=A'E,
∴四边形ADA'E是菱形,
∴AC∥DA',
∴∠BDA'=∠BAC,
又∵∠BAC≠∠ABC,
∴∠BDA'≠∠ABC,
∵∠BAC≠∠C,
∴∠BDA'≠∠C,
∴有且只有当BD=A'D时,△BDA'∽△BAC,
∴当BD=A'D,即5-x=x时,x=![]() .
.
(3)第一种情况:∠BDA'=90°,
∵∠BDA'=∠BAC,而∠BAC≠90°,
∴∠BDA'≠90°.
第二种情况:∠BA'D=90°,
∵在Rt△BA'D中,DB2-A'D2=A'B2,
在Rt△BA'M中,A'M2+BM2=A'B2,
∴DB2-A'D2=A'M2+BM2,
∴(5-x)2-x2=(4-![]() x)2+(3)2,
x)2+(3)2,
解得x=![]() ;
;
第三种情况:∠A'BD=90°,
∵∠A'BD=90°,∠AMB=90°,
∴△BA'M∽△ABM,
即![]() ,
,
∴BA'=![]() ,
,
在Rt△DBA'中,DB2+A'B2=A'D2,
(5-x)2+![]() =x2,
=x2,
解得:x=![]() .
.
综上可知当x=![]() 或
或![]() 时,△A'DB是直角三角形.
时,△A'DB是直角三角形.
-
科目: 来源: 题型:
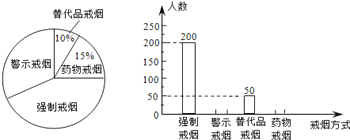
查看答案和解析>>【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年国庆节放假八天,高速公路免费通行,各地风景区游人如织.其中闻名于世的北京故宫在10月1日的游客人数就已经达到了7万人,接下来的七天中,每天的游客人数变化(单位:万人)如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):

(1)10月3日的人数为万人;
(2)这八天,游客人数最多的是10月日,达到万人;游客人数最少的是10月日,为万人;
(3)这8天参观故宫的总人数约为万人(结果精确到万位)
(4)如果你们一家人打算在下一个国庆节参观故宫,请你对你们的出行日期提一个建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(1)这个用户12月用水量10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正方形,
是正方形,  是
是 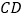 垂直平分线上的点,点
垂直平分线上的点,点 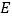 关于
关于 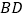 的对称点是
的对称点是 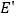 ,直线
,直线 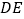 与直线
与直线 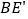 交于点
交于点 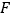 .
.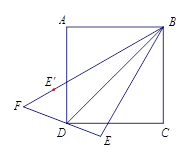
(1)若点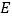 是
是 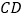 边的中点,连接
边的中点,连接 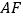 ,则
,则 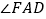 =;
=;
(2)小明从老师那里了解到,只要点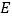 不在正方形的中心,则直线
不在正方形的中心,则直线 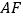 与
与 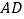 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 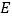 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.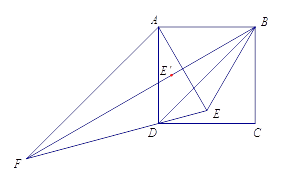
如图,将点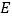 选在正方形内,且△
选在正方形内,且△ 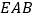 为等边三角形,求出直线
为等边三角形,求出直线 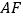 与
与 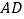 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线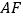 与
与 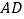 所夹锐角度数的思路.
所夹锐角度数的思路.
相关试题

