【题目】如图16,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=![]()
![]() +k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.
+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是________.

参考答案:
【答案】-2<k<![]() .
.
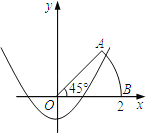
【解析】由图可知,∠AOB=45°,∴直线OA的解析式为y=x,联立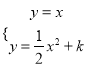 ,消掉y得,x2﹣2x+2k=0,△=b2﹣4ac=(﹣2)2﹣4×1×2k=0,即k=
,消掉y得,x2﹣2x+2k=0,△=b2﹣4ac=(﹣2)2﹣4×1×2k=0,即k=![]() 时,抛物线与OA有一个交点,此交点的横坐标为1,∵点B的坐标为(2,0),∴OA=2,∴点A的坐标为(
时,抛物线与OA有一个交点,此交点的横坐标为1,∵点B的坐标为(2,0),∴OA=2,∴点A的坐标为(![]() ,
, ![]() ),∴交点在线段AO上;当抛物线经过点B(2,0)时,
),∴交点在线段AO上;当抛物线经过点B(2,0)时, ![]() ×4+k=0,解得k=﹣2,∴要使抛物线y=
×4+k=0,解得k=﹣2,∴要使抛物线y=![]() x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是﹣2<k<
x2+k与扇形OAB的边界总有两个公共点,实数k的取值范围是﹣2<k<![]() .故答案为:
.故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCO中,O为坐标原点,A在y轴上,C在x轴上,B的坐标为(8,6),P是线段BC上动点,点D是直线y=2x﹣6上第一象限的点,若△APD是等腰直角三角形,则点D的坐标为_____________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+mx﹣6=0的一个根为2,则m= , 另一个根是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中有两个相等实数根的是( )
A.x2﹣1=0
B.(x+2)2=0
C.x2+3=0
D.(x﹣3)(x+5)=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】用公式法解﹣x2+3x=1时,先求出a、b、c的值,则a、b、c依次为( )
A.﹣1,3,1B.1,3,1C.﹣1,3,﹣1D.1,﹣3,﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2先向右平移2个单位,再向下平移3个单位,那么所得到抛物线的函数关系式是( )
A.y=(x﹣2)2﹣3
B.y=(x+2)2﹣3
C.y=(x﹣2)2+3
D.y=(x+2)2+3 -
科目: 来源: 题型:
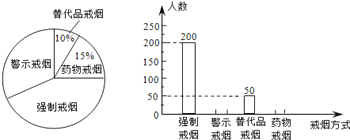
查看答案和解析>>【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
相关试题

