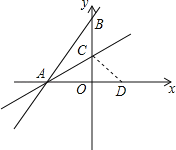
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于A、B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则:
x+4与x轴、y轴分别交于A、B两点,点C在OB上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则:

(1)线段AB的长是 .
(2)点C的坐标是 .
参考答案:
【答案】(1)5(2)(0,1.5).
【解析】
试题分析:(1)先求出OA、OB,再利用勾股定理即可解决问题.
(2)设OC=x,在Rt△COD中,利用勾股定理列出方程即可解决问题.
解:(1)令x=0,得到y=4,令y=0,得到x=﹣3,
∴A(﹣3,0),B(0,4),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=![]() =
=![]() =5,
=5,
(2)设OC=x,在Rt△COD中,OD=2,CD=4﹣x,OC=x,
∵CD2=OC2+OD2,
∴(4﹣x)2=x2+22,
解得x=1.5,
∴点C坐标(0,1.5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角。其中正确的有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校团委组织65名团员为学校建花坛搬砖,七年级的团员每人搬6块砖,其他年级的团员每人搬8块,总共搬了460块砖,问参加搬砖七年级的团员有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=k1x+b(k1为常数,且k1≠0)的图象与反比例函数y2=
 (k2为常数,且k2≠0)的图象相交于A(1,2),B(m,﹣1)两点.
(k2为常数,且k2≠0)的图象相交于A(1,2),B(m,﹣1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若A1(m1,n1),A(m2,n2),A3(m3,n3)为反比例函数图象上的三点,且m1<m2<0<m3,请直接写出n1、n2、n3的大小关系式;
(3)结合图象,请直接写出关于x的不等式k1x+b>
 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
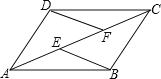
求证:(1)△ADF≌△CBE;
(2)EB∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
(1)补全△A′B′C′
(2)画出AC边上的中线BD;
(3)画出AC边上的高线BE;
(4)求△ABD的面积 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2x2﹣8=
相关试题

