【题目】已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．

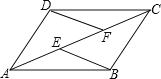
求证：（1）△ADF≌△CBE；

（2）EB∥DF．

参考答案：

【答案】证明见解析

【解析】

试题分析：要证△ADF≌△CBE，因为AE=CF，则两边同时加上EF，得到AF=CE，又因为ABCD是平行四边形，得出AD=CB，∠DAF=∠BCE，从而根据SAS推出两三角形全等，由全等可得到∠DFA=∠BEC，所以得到DF∥EB．

证明：（1）∵AE=CF，

∴AE+EF=CF+FE，即AF=CE．

又ABCD是平行四边形，

∴AD=CB，AD∥BC．

∴∠DAF=∠BCE．

在△ADF与△CBE中，

∴△ADF≌△CBE（SAS）．

（2）∵△ADF≌△CBE，

∴∠DFA=∠BEC．

∴DF∥EB．

关闭