【题目】将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有﹣个小朋友分到苹果但不到8个苹果.求这一箱苹果的个数与小朋友的人数.若设有x人,则可列不等式为( )
A.8(x﹣1)<5x+12<8
B.0<5x+12<8x
C.0<5x+12﹣8(x﹣1)<8
D.8x<5x+12<8
参考答案:
【答案】C
【解析】解:设有x人,则苹果有(5x+12)个,由题意得:
0<5x+12﹣8(x﹣1)<8,
故选:C.
-
科目: 来源: 题型:
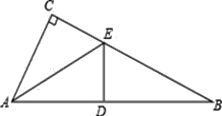
查看答案和解析>>【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.
(1)如果AC=3cm,求AB的长度;
(2)猜想:ED与AB的位置关系,并证明你的猜想。
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
一户居民一个月用电量的范围
电费价格(单位:元/度)
不超过200度
a
超过200度的部分
b
已知4月份,该市居民甲用电250度,交电费130元;居民乙用电400度,交电费220元.
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元? -
科目: 来源: 题型:
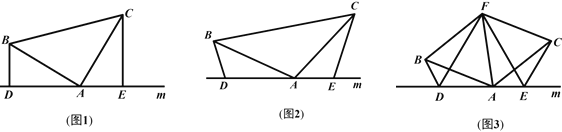
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x(x﹣3)=3﹣x的根是( )
A.﹣1
B.3
C.﹣1和3
D.1和2 -
科目: 来源: 题型:
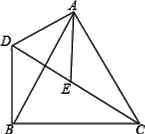
查看答案和解析>>【题目】如图,△ACB和△ADE均为等边三角形,点C、E、D在同一直线上,在△ACD中,线段AE是CD边上的中线,连接BD.求证:CD=2BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个整式中,不能表示图中阴影部分面积的是( )
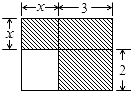
A.(x+3)(x+2)﹣2x
B.x(x+3)+6
C.3(x+2)+x2
D.x2+5x
相关试题

