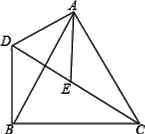
【题目】如图,△ACB和△ADE均为等边三角形,点C、E、D在同一直线上,在△ACD中,线段AE是CD边上的中线,连接BD.求证:CD=2BD.
参考答案:
【答案】证明见解析.
【解析】试题分析:根据已知条件用“SAS”定理证明△ACE≌△ABD,可得BD=CE,由AE是CD边上的中线,可得CD=2CE,从而可证CD=2BD.
试题解析:(1)∵△ACB和△ADE均为等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠CAE=∠BAD,
在△ACE和△ABD中,
AB=AC,∠CAE=∠BAD,AD=AE,
∴△ACE≌△ABD(SAS),
∴BD=CE,
又∵AE是CD边上的中线,
∴CD=2CE,
∴CD=2BD.
-
科目: 来源: 题型:
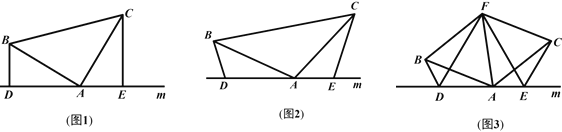
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有﹣个小朋友分到苹果但不到8个苹果.求这一箱苹果的个数与小朋友的人数.若设有x人,则可列不等式为( )
A.8(x﹣1)<5x+12<8
B.0<5x+12<8x
C.0<5x+12﹣8(x﹣1)<8
D.8x<5x+12<8 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x(x﹣3)=3﹣x的根是( )
A.﹣1
B.3
C.﹣1和3
D.1和2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个整式中,不能表示图中阴影部分面积的是( )
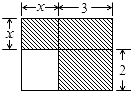
A.(x+3)(x+2)﹣2x
B.x(x+3)+6
C.3(x+2)+x2
D.x2+5x -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形花圃边长增加2cm,所得新正方形花圃的周长是28cm,则:原正方形花圃的边长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】六十四名学生外出参加竞赛,共租车10辆,其中大车每辆可坐8人,小车每辆可坐4人,则大、小车各租多少辆?
相关试题

