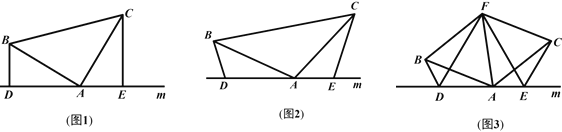
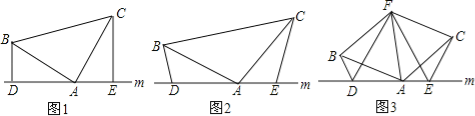
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
参考答案:
【答案】(1)证明见解析;(2)成立,证明见解析;(3)△DEF是等边三角形.证明见解析.
【解析】试题分析:(1)利用已知得出∠CAE=∠ABD,进而利用AAS得出则△ABD≌△CAE,即可得出DE=BD+CE;
(2)根据∠BDA=∠AEC=∠BAC=α,得出∠CAE=∠ABD,在△ADB和△CEA中,根据AAS证出△ADB≌△CEA,从而得出AE=BD,AD=CE,即可证出DE=BD+CE;
(3)与前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,
利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.则
DF=EF.
解:(1)DE=BD+CE.理由如下:
如图1,∵BD⊥l,CE⊥l,
∴∠BDA=∠AEC=90°
又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ABD和△CAE中,
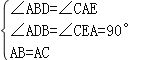 ,
,
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE,
∵DE=AD+AE,
∴DE=CE+BD;
(2)如图2,∵∠BDA=∠AEC=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
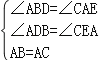 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴BD+CE=AE+AD=DE;
(3)DF=EF.理由如下:
由(2)知,△ADB≌△CAE,
BD=EA,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵BF=AF
在△DBF和△EAF中,
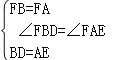 ,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.
∴DF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知|a﹣2|+(b+1)2=0,求﹣(3a2﹣4ab)+[b2﹣2(2a2+2ab)]的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期实验中学组织开展课外兴趣活动,各活动小班根据实际情况确定了计划组班人数,并发动学生自愿报名,报名人数与计划人数的前5位情况如下.若用同一小班的报名人数与计划人数的比值大小来衡量进入该班的难易程度,则由表中数据,可预测( )
小班名称
奥数
写作
舞蹈
篮球
航模
报名人数
215
201
154
76
65
小班名称
奥数
舞蹈
写作
合唱
书法
计划人数
120
100
90
80
70
A.奥数比书法容易
B.合唱比篮球容易
C.写作比舞蹈容易
D.航模比书法容易 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果+3吨表示运入仓库的大米吨数, 那么运出5吨大米表示为( )
A.-3吨 B.+3吨 C.-5吨 D.+5吨
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三个不相等的有理数的和为0,则下列结论正确的是 ( )
A. 三个加数全是0 B. 至少有两个加数是负数
C. 至少有一个加数是负数 D. 至少有两个加数是正数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,△ABC各顶点的横、纵坐标都是整数,直线m上各点的横坐标都为﹣1.
(1)作出△ABC关于直线m的对称图形△A1B1C1;
(2)作出△ABC关于x轴对称的图形△A2B2C2;
(3)写出△A2B2C2的各顶点的坐标.

相关试题

