【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价(元/件) | 6 | 5.2 | 6.5 |
B产品单价(元/件) | 3.5 | 4 | 3 |
并求得了A产品三次单价的平均数和方差:![]() =5.9,SA2=
=5.9,SA2= ![]() [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]= ![]()
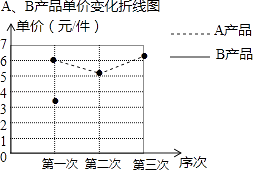
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
参考答案:
【答案】
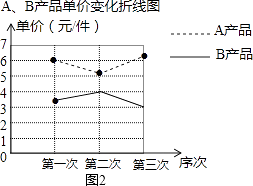
(1)解:如图2所示:
(2)解: ![]() =
= ![]() (3.5+4+3)=3.5,S
(3.5+4+3)=3.5,S ![]() =
= ![]() =
= ![]() ,
,
∵B产品的方差小,
∴B产品的单价波动小;
(3)解:第四次调价后,对于A产品,这四次单价的中位数为 ![]() =
= ![]() ;
;
对于B产品,∵m>0,
∴第四次单价大于3,
∵第四次单价小于4,
∴ ![]() ×2﹣1=
×2﹣1= ![]() ,
,
∴m=25.
【解析】(1)依据表示中B产品的单价补全折线统计图即可;
(2)分别依据平均数公式和方差公式进行计算即可;
(3)首先确定这四次单价的中位数,然后确定第四次调价的范围,最后再根据“A产品这四次单价的中位数是B产品四次单价中位数的2倍少1”列出关于m的方程,从而可求得m的值.
-
科目: 来源: 题型:
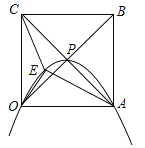
查看答案和解析>>【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系,①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
-
科目: 来源: 题型:
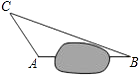
查看答案和解析>>【题目】在一次课外实践活动中,同学们要知道校园内A,B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=120°,请计算A,B两处之间的距离.
-
科目: 来源: 题型:
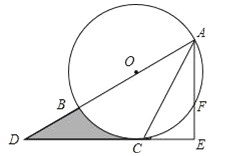
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列图形绕其对角线的交点顺时针旋转90°,所得图形一定与原图形重合的是( )
A.平行四边形B.矩形C.正方形D.菱形
-
科目: 来源: 题型:
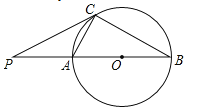
查看答案和解析>>【题目】如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣2)3﹣( )﹣1+(
)﹣1+( 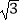 ﹣1)0+(﹣
﹣1)0+(﹣  )2017×(1.5)2016
)2017×(1.5)2016
(2)(2a+1)(2a﹣1)﹣(a+2)2﹣3a(a+1)
(3)(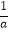 ﹣1)÷
﹣1)÷ 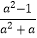 .
.
相关试题

