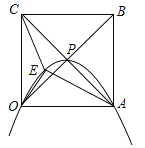
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系,①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值.
参考答案:
【答案】(1)①O(0,0),A(4,0),P(2,2);②![]() ;(2)9.
;(2)9.
【解析】
试题分析:(1)以O点为原点,线段OA所在的直线为x轴,线段OC所在的直线为y轴建立直角坐标系,如图所示.
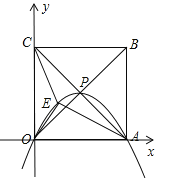
①∵正方形OABC的边长为4,对角线相交于点P,∴点O的坐标为(0,0),点A的坐标为(4,0),点P的坐标为(2,2).
②设抛物线L的解析式为![]() ,∵抛物线L经过O、P、A三点,∴
,∵抛物线L经过O、P、A三点,∴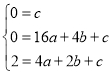 ,解得:
,解得: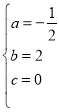 ,∴抛物线L的解析式为
,∴抛物线L的解析式为![]() ;
;
(2)∵点E是正方形内的抛物线上的动点,∴设点E的坐标为(m,![]() )(0<m<4),∴S△OAE+SOCE=
)(0<m<4),∴S△OAE+SOCE=![]() OAyE+
OAyE+![]() OCxE=
OCxE=![]() =
=![]() ,∴当m=3时,△OAE与△OCE面积之和最大,最大值为9.
,∴当m=3时,△OAE与△OCE面积之和最大,最大值为9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+1与2﹣x成正比,且当x=﹣1时,y=5,则y与x的函数关系是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两个变量x、y不是反比例的关系是( )
A.书的单价为12元,售价y(元)与书的本数x(本)
B.xy=7
C.当k=﹣1时,式子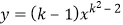 中的y与x
中的y与x
D.小亮上学用的时间x(分钟)与速度y(米/分钟) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:(1)(2)
(1)计算: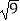 ﹣(﹣2)+(﹣1)0﹣(
﹣(﹣2)+(﹣1)0﹣(  )﹣1+
)﹣1+ 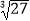
(2)比较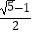 与0.5的大小.
与0.5的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课外实践活动中,同学们要知道校园内A,B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=120°,请计算A,B两处之间的距离.
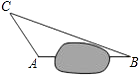
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
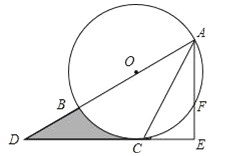
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
并求得了A产品三次单价的平均数和方差:
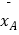 =5.9,SA2=
=5.9,SA2=  [(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]=
[(6﹣5.9)2+(5.2﹣5.9)2+(6.5﹣5.9)2]= 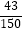
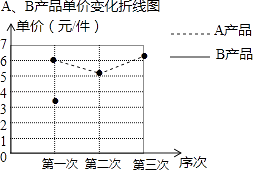
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
相关试题

