【题目】某城市自来水收费实行阶梯水价,收费标准如下表所示:

(1)某用户四月份用水量为16吨,需交水费为多少元?
(2)某用户五月份交水费50元,所用水量为多少吨?
(3)某用户六月份用水量为a吨,需要交水费为多少元?
参考答案:
【答案】(1)34元;(2)21![]() 吨;(3)见解析
吨;(3)见解析
【解析】
试题分析:(1)首先得出16吨,应分两段交费,再利用已知表格中数据求出答案;
(2)利用五月份交水费50元,可以判断得出应分3段交费,再利用已知表格中数据得出等式求出答案;
(3)利用分类讨论利用①当a≤12时,②当12<a≤18时,③当a>18时,求出答案.
解:(1)∵12<16<18,
∴2×12+2.5×(16﹣12)
=24+10
=34(元),
答:四月份用水量为16吨,需交水费为34元;
(2)设五月份所用水量为x吨,依据题意可得:
2×12+6×2.5+(x﹣18)×3=50,
解得;x=21![]() ,
,
答:五月份所有水量为21![]() 吨;
吨;
(3)①当a≤12时,需交水费2a元;
②当12<a≤18时,需交水费,2×12+(a﹣12)×2.5=(2.5a﹣6)元,
③当a>18时,需交水费2×12+6×2.5+(a﹣18)×3=(3a﹣15)元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)

(1)数轴上点B对应的数是______.
(2)经过几秒,恰好使AM=2BN?
(3)经过几秒,点M、点N分别到原点O的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的口袋中放着若干个黄球和绿球,这两种球除了颜色之外没有其它任何区别,袋中的球已经搅匀,从口袋中取出一个球取出黄球的概率为
 .
.(1)取出绿球的概率是多少?
(2)如果袋中的黄球有12个,那么袋中的绿球有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料1:一般地,
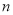 个相同因数
个相同因数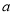 相乘:
相乘: 记为
记为 .如
.如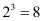 ,此时,3叫做以2为底的8的对数,记为
,此时,3叫做以2为底的8的对数,记为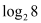 (即
(即 ).那么,
).那么, ,
, .
.材料2:新规定一种运算法则:自然数1到n的连乘积用n!表示,例如:1!=1 ,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…在这种规定下,请你解决下列问题:
(1)计算 5!= ;
(2)已知x为整数 ,求出满足该等式的x:
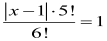
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD=BE,DG⊥BC于G,EF⊥BG交BC于F,且DG=EF.

(1)△DGC与△EFB全等吗?请说明理由;
(2)OB=OC吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
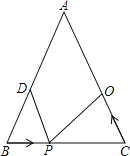
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
(3)若∠C=70°,当∠CPQ的度数为多少时,△CPQ为等腰三角形?(请直接写出答案,不必写出过程).
相关试题

