【题目】在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
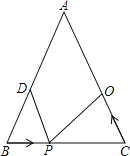
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
(3)若∠C=70°,当∠CPQ的度数为多少时,△CPQ为等腰三角形?(请直接写出答案,不必写出过程).
参考答案:
【答案】(1)![]() cm/s;(2)当P出发2.5秒或10秒后,△BPD为直角三角形;(3)当△CPQ为等腰三角形时,∠CPQ的度数为35°,40°,55°,70°.
cm/s;(2)当P出发2.5秒或10秒后,△BPD为直角三角形;(3)当△CPQ为等腰三角形时,∠CPQ的度数为35°,40°,55°,70°.
【解析】
试题分析:(1)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
(2)分两种情况;①当∠BPD=90°时,由∠B=60°,得到∠BDP=30°,求得2BP=BD=10,求出x=2.5;②当∠BDP=90°时,根据三角形的内角和得到∠BPD=30°,求出x=10;即可得到当P出发2.5秒或10秒后,△BPD为直角三角形;
(3)分点P在边BC上或点P在边BC的延长线上,△CPQ为等腰三角形,根据等腰三角形的性质和三角形的内角和即可得到结论.
解:(1)∵AB=AC,
∴∠B=∠C,
∵AB=20cm,D是AB的中点,
∴BD=10cm,
∵点Q的速度与点P的速度不同,
∴BP≠CQ,
要使△BPD和△CQP全等,
则BP=CP=8cm CQ=BD=10cm,
∴x=![]() 秒,
秒,
∴a=![]() =
=![]() cm/s;
cm/s;
(2)①当∠BPD=90°时,
∵∠B=60°,∴∠BDP=30°,
∴2BP=BD=10,
∴BP=5,
即2x=5,
∴x=2.5;
②当∠BDP=90°时,
∵∠B=60°,
∴∠BPD=30°,
∴BP=2BD=20,
即2x=20,
∴x=10;
∴当P出发2.5秒或10秒后,△BPD为直角三角形;
(3)点P在边BC上,△CPQ为等腰三角形,
①当PQ=CQ,∵∠C=70°,
∴∠CPQ=∠C=70°,
②当PQ=PC,∵∠C=70°,
∴∠PQC=∠C=70°,
∴∠CPQ=180°﹣2×70°=40°,
③当PC=CQ,∵∠C=70°,
∴∠CPQ=∠CQP=![]() =55°,
=55°,
点P在边BC的延长线上,△CPQ为等腰三角形,
∵∠ACB=70°,∴∠ACP=110°,
∵PC=CQ,
∴∠CPQ=∠CQP=![]() =35°,
=35°,
综上所述:当△CPQ为等腰三角形时,∠CPQ的度数为35°,40°,55°,70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市自来水收费实行阶梯水价,收费标准如下表所示:

(1)某用户四月份用水量为16吨,需交水费为多少元?
(2)某用户五月份交水费50元,所用水量为多少吨?
(3)某用户六月份用水量为a吨,需要交水费为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD=BE,DG⊥BC于G,EF⊥BG交BC于F,且DG=EF.

(1)△DGC与△EFB全等吗?请说明理由;
(2)OB=OC吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】瓦甸科星化工有限公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.请根据图中提供的信息解答下列问题

(1)这次共调查了多少名学生?扇形统计图中方案1所对应的圆心角的度数为多少度?
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?
-
科目: 来源: 题型:
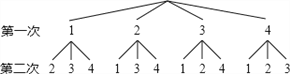
查看答案和解析>>【题目】在不透明的袋子中有四张标着数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏.小明画出树状图如图所示:
小华列出表格如下:
1
2
3
4
1
(1,1)
(2,1)
(3,1)
(4,1)
2
(1,2)
(2,2)
①
(4,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(1)根据树形图分析,小明的游戏规则是,随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;根据表格分析,小华的游戏规则是,随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片。
(2)根据小华的游戏规则,表格中①表示的有序数对为 。
(3)规定两次抽到的数字之和为奇数的获胜,谁获胜的可能性大?为什么?
相关试题

