【题目】如图1是一个长为 ![]() ,宽为
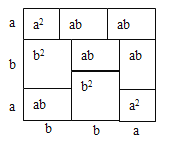
,宽为 ![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出 ![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)根据(2)中的结论,若 ![]() ,
,![]() ,则
,则 ![]() ;
;
(4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式![]() .在图形上把每一部分的面积标写清楚.
.在图形上把每一部分的面积标写清楚.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)±5;(4)详见解析
;(3)±5;(4)详见解析
【解析】
(1)表示出阴影部分正方形的边长,然后根据正方形的面积公式列式即可;
(2)根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可;
(3)将(x-y)2变形为(x+y)2—4xy,再代入求值即可;
(4)由已知的恒等式,画出相应的图形,如图所示.
解:(1)阴影部分为一个正方形,其边长为b-a,
∴其面积为:![]() ,
,
故答案为:![]() ;
;
(2)大正方形面积为:![]()
小正方形面积为:![]() =
=![]() ,
,
四周四个长方形的面积为:![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(3)由(2)知,![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
故答案为:±5;
(4)符合等式![]() 的图形如图所示,
的图形如图所示,
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:对于二次三项式
 ,能直接用公式法进行因式分解,得到
,能直接用公式法进行因式分解,得到  ,但对于二次三项式
,但对于二次三项式  ,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式
,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式  中先加上一项
中先加上一项  ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去  这项,使整个式子的值不变,于是:
这项,使整个式子的值不变,于是:
像这样把二次三项式分解因式的方法叫做添(拆)项法.
 问题解决:请用上述方法将二次三项式
问题解决:请用上述方法将二次三项式  分解因式.
分解因式.(2)拓展应用:二次三项式
 有最小值或有最大值吗?如果有,请你求出来并说明理由.
有最小值或有最大值吗?如果有,请你求出来并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.如果∠BAC=30°,∠DAE=105°,则y与x之间的函数关系式为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点P(﹣3,0),且与两坐标轴截得的三角形面积为4,则此一次函数的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结
 、
、 两点的线段就是
两点的线段就是 、
、 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
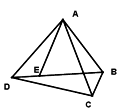
①试说明BE·AD=CD·AE;
②根据图形特点,猜想 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
相关试题

