【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
参考答案:
【答案】
(1)解:把A(﹣2,1)代入y= ![]() ,得m=﹣2,
,得m=﹣2,
即反比例函数为y=﹣ ![]() ,则n=
,则n= ![]() n=﹣2,
n=﹣2,
即B(1,﹣2),把A(﹣2,1),B(1,﹣2)代入y=kx+b,
求得k=﹣1,b=﹣1,所以y=﹣x﹣1
(2)解:由图象可知:x<﹣2或0<x<1
【解析】先将点A的坐标代入反比例函数解析式,建立方程求出反比例函数的解析式,再将点B的坐标代入求出n的值,再利用待定系数法将A、B两点坐标代入一次函数解析式,求出结果。
(2)要求一次函数值大于反比例函数值,要看直线x-=1,直线x=-2,y轴,三条直线将两函数分成四部分,观察一次函数图象在反比例函数图象上方时所对应的x的取值范围即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.如果∠BAC=30°,∠DAE=105°,则y与x之间的函数关系式为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点P(﹣3,0),且与两坐标轴截得的三角形面积为4,则此一次函数的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为
 ,宽为
,宽为  的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出
 ,
, ,
, 之间的等量关系是 ;
之间的等量关系是 ;(3)根据(2)中的结论,若
 ,
, ,则
,则  ;
;(4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式
 .在图形上把每一部分的面积标写清楚.
.在图形上把每一部分的面积标写清楚. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结
 、
、 两点的线段就是
两点的线段就是 、
、 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
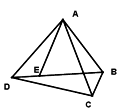
①试说明BE·AD=CD·AE;
②根据图形特点,猜想 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,有四个点A(﹣8,3)、B(﹣4,5)、C(0,n)、D(m,0),当四边形ABCD的周长最短时,求
 的值.
的值.
相关试题

