Question

【题目】如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE.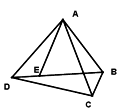

①试说明BE·AD＝CD·AE；
②根据图形特点，猜想 可能等于哪两条线段的比?并证明你的猜想，（只须写出有线段的一组即可）

Answer 1

【答案】解：①∵∠BAC=∠DAE，

∴∠BAC+∠CAE=∠DAE+∠CAE，

即∠DAC=∠BAE，

∵∠AEB=∠ADB+∠DAE，

∠ADC=∠ADB+∠BDC，

又∵∠DAE=∠BDC，

∴∠AEB=∠ADC，

∴△BEA∽△CDA，

∴ = ，

即BE·AD=CD·AE；

②猜想 = 或（ ），

由△BEA∽△CDA可知， = ，即 = ，

又∵∠DAE=∠BAC，

∴△BAC∽△EAD，

∴ = 或（ ）

【解析】①根据∠BAC=∠DAE证明∠DAC=∠BAE，再根据三角形的外角性质得出∠AEB=∠ADB+∠DAE，∠ADC=∠ADB+∠BDC，由∠BDC＝∠DAE，证出∠AEB=∠ADC，然后根据两组角对应相等的两三角形相似，得对应边成比例，即可证得结论。
（2）根据已知证明△BEA∽△CDA和△BAC∽△EAD，即可得出结论。
【考点精析】利用三角形的外角和相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知三角形一边与另一边的延长线组成的角，叫三角形的外角；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．