【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

参考答案:
【答案】(1)40,20;(2) 20;(3)详见解析
【解析】
(1)根据三角形的高求出∠ADC=90°,再根据三角形内角和定理求出求出∠BAC和∠DAC,根据角平分线定义求出∠CAE,即可求出答案;
(2)根据三角形的高求出∠ADC=90°,再根据三角形内角和定理求出求出∠BAC和∠DAC,根据角平分线定义求出∠CAE,即可求出答案;
(3)根据三角形的高求出∠ADC=90°,再根据三角形内角和定理求出求出∠BAC和∠DAC,根据角平分线定义求出∠CAE,最后代入求出即可.
解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°-(∠B+∠C)=80°,
∵AE是角平分线,
∴∠CAE=![]() =40°,
=40°,
∵AD是高,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°-∠ADC-∠C=20°,
∴∠DAE=∠CAE-∠CAD=40°-20°=20°,
故答案为:40,20;
(2)∵∠B=40°,∠C=80°,
∴∠BAC=180°-(∠B+∠C)=60°,
∵AE是角平分线,
∴∠CAE=![]() =30°,
=30°,
∵AD是高,
∴∠ADC=90°,
∵∠C=80°,
∴∠DAC=180°-∠ADC-∠C=10°,
∴∠DAE=∠CAE-∠CAD=30°-10°=20°,
故答案为:20;
(3)∵∠BAC +∠B+∠C=180°,
∴∠BAC=180°-(∠B+∠C),
∵AE是角平分线,
∴∠CAE=![]()
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∴∠DAE=∠CAE-∠CAD
![]()
![]()
![]()
![]()
=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, ,
,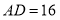 ,
, ,
,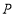 是射线
是射线 上一点,连接
上一点,连接 ,沿
,沿 将
将 折叠,得
折叠,得 .
.(1)如图所示,当
 时,
时, _______度;
_______度;
(2)如图所示,当
 时,求线段
时,求线段 的长度;
的长度;
(3)当点
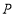 为
为 中点时,点
中点时,点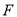 是边
是边 上不与点
上不与点 、
、 重合的一个动点,将
重合的一个动点,将 沿
沿 折叠,得到
折叠,得到 ,连接
,连接 ,求
,求 周长的最小值.
周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )

A.8对B.7对C.6对D.5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业用规格是170×40的标准板材作为原材料,按照如图1所示的裁法一或裁法二,裁剪出甲型与乙型两种板材(单位:cm)

(1)求图中a,b的值;
(2)若将50张标准板材按裁法一裁剪,10张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图2的竖式与横式两种无盖的装饰盒若干(接缝处的长度忽略不计).

①一共可裁剪出甲型板材______张,乙型板材______张;
②设可以做出竖式和横式两种无盖装饰盒一共x个,则x的最大值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个直角三角形纸板ABC放置在锐角△PMN上,使该直角三角形纸板的两条直角边AB,AC分别经过点M,N.
(发现)
(1)如图1,若点A在△PMN内,当∠P=30°时,则∠PMN+∠PNM=______°,∠AMN+∠ANM=______°,∠PMA+∠PNA=______°.
(2)如图2,若点A在△PMN内,当∠P=50°时,∠PMA+∠PNA=______°.
(探究)
(3)若点A在△PMN内,请你判断∠PMA,∠PNA和∠P之间满足怎样的数量关系,并写出理由.
(应用)
(4)如图3,点A在△PMN内,过点P作直线EF∥AB,若∠PNA=16°,则∠NPE=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】市场调查表明:某种一周内水果的销售率y(销售率=
 )与价格倍数x(价格倍数=
)与价格倍数x(价格倍数=  )的关系满足函数关系y=﹣
)的关系满足函数关系y=﹣  x+
x+  (1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120%
B.80%
C.60%
D.40%
相关试题

