【题目】如图,在△ABC中,AB=AC,高BD,CE交于点O,AO交BC于点F,则图中共有全等三角形( )

A.8对B.7对C.6对D.5对
参考答案:
【答案】B
【解析】
易证△ABC是关于AF对称的图形,其中的小三角形也关于AF对称,共可找出7对三角形.
全等的三角形有:①△AFB≌△AFC;②△CEB≌△BDC;③△AEO≌△ADO;④△EOB≌△DOC;⑤△OBF≌△OFC;⑥△AOB≌△AOC;⑦△AEC≌△ADB
证明①△AFB≌△AFC
∵AB=AC,CE⊥AB,BD⊥AC
又∵![]()
∴CE=BD
∴在Rt△BCE和Rt△CBD中
![]()
∴△BCE≌△CBD
∴BE=CD,∴AE=AD
在Rt△AEO和Rt△ADO中
![]()
∴△AEO≌△ADO
∴∠EOD=∠DOA
在△BAF和△CAF中

∴△BAF≌△CAF,得证
其余全等证明过程类似
故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,…,为了投资少而获利大,每个每天应提高( )
A.4元或6元
B.4元
C.6元
D.8元 -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个一次函数与
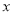 轴的交点关于
轴的交点关于 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与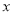 轴的交点为“对心点”.
轴的交点为“对心点”.
(1)写出一个
 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;(2)直线
 经过点
经过点 和
和 ,直线
,直线 的“对心函数”直线
的“对心函数”直线 与
与 轴的交点
轴的交点 位于点
位于点 的上方,且直线
的上方,且直线 与直线
与直线 交于点
交于点 ,点
,点 为直线
为直线 的“对心点”.点
的“对心点”.点 是动直线
是动直线 上不与
上不与 重合的一个动点,且
重合的一个动点,且 ,试探究
,试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.(3)如图,直线
 与其“对心函数”直线
与其“对心函数”直线 的交点
的交点 位于第一象限,
位于第一象限, 、
、 分别为直线
分别为直线 、
、 的“对心点”,点
的“对心点”,点 为线段
为线段 上一点(不含端点),连接
上一点(不含端点),连接 ;一动点
;一动点 从
从 出发,沿线段
出发,沿线段 以
以 单位
单位 秒的速度运动到点
秒的速度运动到点 ,再沿线段
,再沿线段 以
以 单位
单位 秒的速度运动到点
秒的速度运动到点 后停止,点
后停止,点 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为 秒,求直线
秒,求直线 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形
 中,
中, ,
,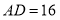 ,
, ,
,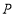 是射线
是射线 上一点,连接
上一点,连接 ,沿
,沿 将
将 折叠,得
折叠,得 .
.(1)如图所示,当
 时,
时, _______度;
_______度;
(2)如图所示,当
 时,求线段
时,求线段 的长度;
的长度;
(3)当点
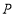 为
为 中点时,点
中点时,点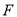 是边
是边 上不与点
上不与点 、
、 重合的一个动点,将
重合的一个动点,将 沿
沿 折叠,得到
折叠,得到 ,连接
,连接 ,求
,求 周长的最小值.
周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是高,AE是角平分线.
(1)若∠B=30°,∠C=70°,则∠CAE=______°,∠DAE=______°.
(2>若∠B=40°,∠C=80°.则∠DAE=______°.
(3)通过探究,小明发现将(2)中的条件“∠B=40°,∠C=80°”改为“∠C-∠B=40°”,也求出了∠DAE的度数,请你写出小明的求解过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业用规格是170×40的标准板材作为原材料,按照如图1所示的裁法一或裁法二,裁剪出甲型与乙型两种板材(单位:cm)

(1)求图中a,b的值;
(2)若将50张标准板材按裁法一裁剪,10张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图2的竖式与横式两种无盖的装饰盒若干(接缝处的长度忽略不计).

①一共可裁剪出甲型板材______张,乙型板材______张;
②设可以做出竖式和横式两种无盖装饰盒一共x个,则x的最大值是______.
相关试题

