搜索
【题目】如图，E为正方形ABCD对角线BD上一点，且BE=BC，则∠DCE= ．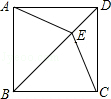 
参考答案：
【答案】22.5°
【解析】解：∵四边形ABCD是正方形， ∴∠CBE=45°，∠BCD=90°，
∵BE=BC，
∴∠BCE= 
（180°﹣∠BCE）= ×（180°﹣45°）=67.5°，
∴∠DCE=∠BCD﹣∠BCE=90°﹣67.5°=22.5°．
所以答案是：22.5°．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过点A（﹣1，0），B（0，﹣
），C（2，0），其对称轴与x轴交于点D（1）求二次函数的表达式及其顶点坐标；
（2）若P为y轴上的一个动点，连接PD，求
PB+PD的最小值；（3）M（x，t）为抛物线对称轴上一动点
①若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，则这样的点N共有 个；
②连接MA，MB，若∠AMB不小于60°，求t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】3月份，某品牌衬衣正式上市销售，3 月1日的销售量为10件，3月2日的销售量为35件，以后每天的销售量比前一天多25件，直到日销售量达到最大后，销售量开始逐日下降，至此，每天的销售量比前一天少15件，直到3月31日销售量为0，设该品牌衬衣的日销量为p（件），销售日期为n（日），p与n之间的关系如图所示。
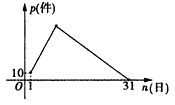
（1）求3月 日时,日销售量最大.
（2）写出p关于n的函数关系式（注明n 的取值范围）；
（3）经研究表明，该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期，请问：该品牌衬衣本月在市面的流行期是多少天？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形ABCD中，∠B=60°，AB=2cm，E、F分别是BC、CD的中点，连接AE、EF、AF，则△AEF的周长为（ ）
A.2
cm
B.3 cm
C.4 cm
D.3cm -
科目： 来源： 题型：
查看答案和解析>>【题目】已知AM∥CN，点B为平面内一点，AB⊥BC于B．
（1）如图1，直接写出∠A和∠C之间的数量关系；
（2）如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；
（3）如图3，在（2）问的条件下，点E、F在DM上，连接BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD相交于点O，点E是CD的中点，BC=10cm．求OE的长．
-
科目： 来源： 题型：
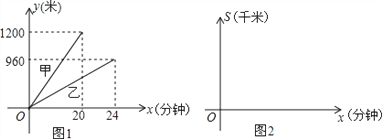
查看答案和解析>>【题目】A,B,C三地依次在一条直线公路上,甲,乙二人分别从A,B两地同时出发沿公路匀速步行到C地,两人离出发地的距离y(米)与出发时间x(分钟)函数图象如图1所示.
(1)甲的步行速度为 米/分钟,乙的步行速度为 米/分钟,A,B两地之间的距离为 米．
(2)设两人离B地的距离为s(米),出发时间x(分钟),请在图(2)中分别画出甲,乙二人s与x的函数图象.
(3)两人出发多长时间离B地距离相等?
相关试题
