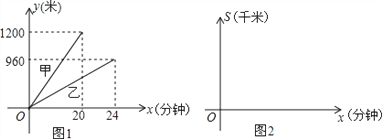
【题目】A,B,C三地依次在一条直线公路上,甲,乙二人分别从A,B两地同时出发沿公路匀速步行到C地,两人离出发地的距离y(米)与出发时间x(分钟)函数图象如图1所示.
(1)甲的步行速度为 米/分钟,乙的步行速度为 米/分钟,A,B两地之间的距离为 米.
(2)设两人离B地的距离为s(米),出发时间x(分钟),请在图(2)中分别画出甲,乙二人s与x的函数图象.
(3)两人出发多长时间离B地距离相等?
参考答案:
【答案】(1)60,40,240;
(2)甲、乙二人s与x的函数图象见解析;
(3)两人出发2.4分或12分钟时离开点B的距离相等.
【解析】(1)根据速度=路程÷时间就可以求出甲、乙的速度,由图象信息可以求出AC、BC的距离;
(2)先用(1)的结论求出甲走到B地的时间,从而可以画出大致
图形;
(3)分别求出好像是,再构成方程组求出其解就可以得出结论.
解:(1)甲的步行速度为:1200÷20=60(米/分钟);
乙的步行速度为:960÷24=40(米/分钟);
A、B两地的距离为:1200-960=240(米);
故答案为:60,40,240;
(2)甲由A到B的时间:240÷60=4(分)
甲,乙二人s与x的图象如图:
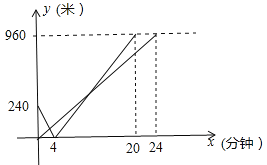
(3)甲经过(4,0)(20,960)设解析式为s1=kx +b
![]() ,解得
,解得![]() ,
,
∴s1=60x-240,
乙经过(0,0),(24,960)设解析式为:s2=mx,
∴960=24m,解得m=40,
∴s2=4ox,
解:40x=60x-240,得x=12,
∴两人出发12分钟在途中相遇.
答:两人出发12分钟在途中相遇.
“点睛”本题考查了速度=路程÷时间的运用,待定系数法求函数的解析式的运用,由点的坐标画函数图象的运用,一次函数与一次方程组的运用,解答时起床一次函数的解析式是关键 .
-
科目: 来源: 题型:
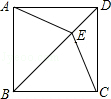
查看答案和解析>>【题目】如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD相交于点O,点E是CD的中点,BC=10cm.求OE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学生对小区居民的健身方式进行调查,并将调查结果绘制成如下两幅不完整的统计图.请根据所给信息解答下列问题:
(1)本次共调查_________人.
(2)补全图(1)中的条形统计图,图(2)中“跑步”所在扇形对应的圆心角度数是_______.
(3)估计2000人中喜欢打太极的大约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】现代有不少世界领先的数学研究成果是以华人数学家命名的,如:有一位数学家的关于完整三角和研究成果被国际数学界称为“华氏定理”,这是以________的姓氏命名的;另一位数学家在仿射微分几何学方面的研究成果在国际上被命为“苏氏锥面”,这是以________的姓氏命名的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=
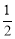 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.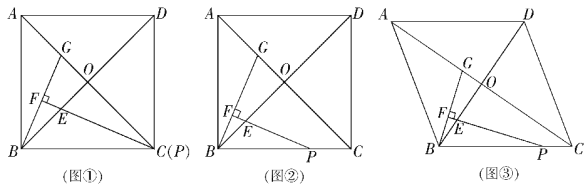
(1) 当点P与点C重合时(如图①).求证:△BOG≌△POE;(4分)
(2)通过观察、测量、猜想:
 = ,并结合图②证明你的猜想;(5分)
= ,并结合图②证明你的猜想;(5分)(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求
 的值.(用含α的式子表示)(5分)
的值.(用含α的式子表示)(5分)
相关试题

