【题目】3月份,某品牌衬衣正式上市销售,3 月1日的销售量为10件,3月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到3月31日销售量为0,设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示。
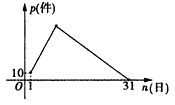
(1)求3月 日时,日销售量最大.
(2)写出p关于n的函数关系式(注明n 的取值范围);
(3)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期,请问:该品牌衬衣本月在市面的流行期是多少天?
参考答案:
【答案】(1)12
(2)p关于n的函数关系式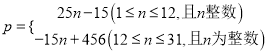
(3)该品牌衬衣本月在市面的流行期是14天.
【解析】(1)因为5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0,所以
(2)分1≤n≤12时和12<n≤31两种情况列出不等式,分别求出n的取值范围即可;
(3)以12日为界,前后是两个等差数列 当 1≤n≤12时,首项a1=10,末项a12=285,项数 k1=12 所以 和 s1=(10+285)×![]() =1770 当 12<n≤31时,首项a13=270,末项a31=0,项数 k2=19 所以 和 s1=270×
=1770 当 12<n≤31时,首项a13=270,末项a31=0,项数 k2=19 所以 和 s1=270×![]() =2565,再求出其和即可.
=2565,再求出其和即可.
解:(1)设3月x是最后一天销售量增加的日期,据题意得,
![]() ,解得
,解得![]()
(2)由(1)得![]() 或
或![]()
(3)当![]() 若
若![]() ,解得
,解得![]() ,考虑实际日期,
,考虑实际日期,
应从7日起算,此段时间流行期为12-7+1=6天
当![]() ,故此段流行期为
,故此段流行期为
20-12=8天。因此6+8=14天
“点睛”本题考查了一次函数的运用,一次函数的图象的意义的运用,求出一次函数的解析式的运用,解答时认真分析,需仔细观察图象,利用分段函数解决问题是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.

(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.

(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣
 ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,求
 PB+PD的最小值;
PB+PD的最小值;(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠B=60°,AB=2cm,E、F分别是BC、CD的中点,连接AE、EF、AF,则△AEF的周长为( )

A.2 cm
cm
B.3 cm
cm
C.4 cm
cm
D.3cm -
科目: 来源: 题型:
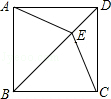
查看答案和解析>>【题目】如图,E为正方形ABCD对角线BD上一点,且BE=BC,则∠DCE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
相关试题

