【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+2x+3与x轴的交点为A,B(点A在点B的左侧),与y轴的交点为C,连结BC.点M是抛物线上A,C之间的一个动点,过点M作MN∥BC,分别交x轴、抛物线于D,N,过点M作EF⊥x轴,垂足为F,并交直线BC于点E,
(1)求点A,B,C的坐标.
(2)当点M恰好是EF的中点,求BD的长.
(3)连接DE,记△DEM,△BDE的面积分别为S1 , S2 , 当BD=1时,则S2﹣S1= .
参考答案:
【答案】
(1)
解:在y=﹣x2+2x+3中,令y=0可得﹣x2+2x+3=0,解得x=﹣1或x=3,
∴A(﹣1,0),B(3,0),
令x=0可得y=3,
∴C(0,3);
(2)
解:∵B(3,0),C(0,3),
∴直线BC解析式为y=﹣x+3,
∵点M是抛物线上A,C之间的一个动点,
∴可设M(t,﹣t2+2t+3)(﹣1<t<0),则E(t,﹣t+3),
∴EF=﹣t+3,MF=﹣t2+2t+3,
∵M为EF的中点,
∴﹣t+3=2(﹣t2+2t+3),解得t=﹣ ![]() 或t=3(不符合题意,舍去),
或t=3(不符合题意,舍去),
∴F(﹣ ![]() ,0),
,0),
∴BF=3﹣(﹣ ![]() )=
)= ![]() ,
,
∵MN∥BC,
∴D为BF的中点,
∴BD= ![]() BF=
BF= ![]() ;
;
(3)![]()
【解析】解:(3)如图,过D作DH∥EF,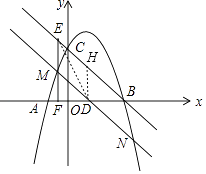
∵MN∥BC,
∴四边形DHEM为平行四边形,
∴S△DEM=S△DEH ,
∵DH⊥BD,且∠OBC=45°,
∴DH=BD=1,
∴S2﹣S1=S△HDB= ![]() BDDH=
BDDH= ![]() ×1×1=
×1×1= ![]() ,
,
所以答案是: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.

(1)求证:AC平分∠DAB;
(2)若点E为 的中点,AD=
的中点,AD=  ,AC=8,求AB和CE的长.
,AC=8,求AB和CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+4A(1,﹣1),B(5,﹣1),与y轴交于点C.

(1)求抛物线的函数表达式;
(2)如图1,连接CB,若点P在直线BC上方的抛物线上,△BCP的面积为15,求点P的坐标;
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为弧ACE上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )

A.15°
B.20°
C.25°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为( ).

A. 9 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=6,BC=8,AD平分∠BAC,则点B到AD的距离是( )

A.3
B.4
C.2
D.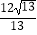
相关试题

