Question

【题目】如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AD⊥CD于点D．
（1）求证：AC平分∠DAB；
（2）若点E为 的中点，AD= ，AC=8，求AB和CE的长．

Answer 1

【答案】
（1）证明：连接OC，

∵直线CD与⊙O相切于点C，

∴OC⊥CD，

∵AD⊥CD，

∴OC∥AD，

∴∠DAC=∠OCA，

∵OA=OC，

∴∠OCA=∠OAC，

∴∠OAC=∠DAC，

即AC平分∠DAB

（2）连接BC，OE，过点A作AF⊥EC于点F，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠ACB=∠ADC，

∵∠DAC=∠BAC，

∴△ADC∽△ACB，

∴ ，

即 ，

解得：AB=10，

∴BC= =6，

∵点E为 的中点，

∴∠AOE=90°，

∴OE=OA= AB=5，

∴AE= =5 ，

∵∠AEF=∠B（同弧所对圆周角相等），∠AFE=∠ACB=90°，

∴△ACB∽△AFE，

∴ ，

∴ ，

∴AF=4 ，EF=3 ，

∵∠ACF= ∠AOE=45°，

∴△ACF是等腰直角三角形，

∴CF=AF=4 ，

∴CE=CF+EF=7 ．

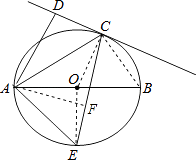
【解析】（1）首先连接OC，由直线CD与⊙O相切于点C，AD⊥CD，易证得OC∥AD，继而可得AC平分∠DAB；（2）首先连接BC，OE，过点A作AF⊥CE于点F，可证得△ADC∽△ACB，△ACB∽△AFE，△ACF是等腰直角三角形，然后由相似三角形的对应边成比例以及勾股定理，即可求得答案．
【考点精析】本题主要考查了等腰直角三角形和勾股定理的概念的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．