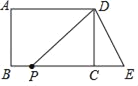
【题目】如图,在长方形ABCD中,AB=6厘米,AD=8厘米.延长BC到点E,使CE=3厘米,连接DE.动点P从B点出发,以2厘米/秒的速度向终点C匀速运动,连接DP.设运动时间为t秒,解答下列问题:
(1)当t为何值时,△PCD为等腰直角三角形?
(2)设△PCD的面积为S(平方厘米),试确定S与t的关系式;
(3)当t为何值时,△PCD的面积为长方形ABCD面积的![]() ?
?
(4)若动点P从点B出发,以2厘米/秒的速度沿BC﹣CD﹣DA向终点A运动,是否存在某一时刻t,使△ABP和△DCE全等?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)t=1秒;(2)S=﹣6t+24(0≤t≤4);(3)t=2秒;(4)t=![]() 秒或
秒或![]() 秒时,△ABP和△DCE全等.
秒时,△ABP和△DCE全等.
【解析】
(1)用含t的式子表示PC,再根据△CDP是等腰直角三角形得到CP=CD=6,解出t即可;(2)利用S△PCD=![]() CP×CD即可求解;(3)根据面积的关系即可列式求解;(4)根据对应点不同分两种情况讨论即可求解.
CP×CD即可求解;(3)根据面积的关系即可列式求解;(4)根据对应点不同分两种情况讨论即可求解.
(1)在长方形ABCD中,AB=6厘米,AD=8厘米,
∴BC=AD=8cm,CD=AB=6cm,∠DCB=∠DCE=90°,
由运动知,BP=2t,
∴PC=BC﹣BP=8﹣2t,
∴△CDP是等腰直角三角形,
∴CP=CD=6,
∴8﹣2t=6,
∴t=1秒,
(2)由(1)知,PC=8﹣2t,
∴S=S△PCD=![]() CP×CD=
CP×CD=![]() (8﹣2t)×6=﹣6t+24(0≤t≤4);
(8﹣2t)×6=﹣6t+24(0≤t≤4);
(3)∵AB=6,AD=8,
∴S长方形ABCD=6×8=48cm2,
由(2)知,S=﹣6t+24(0≤t≤4),
∵△PCD的面积为长方形ABCD面积的![]() ,
,
∴﹣6t+24=![]() ×48,
×48,
∴t=2秒,
(4)在△ABP中,AB=6cm,在△CDE中,CD=6cm,
∴AB=CD,
∵△ABP和△DCE全等,
∴△ABP≌△DCE或△ABP≌△CDE,
当△ABP≌△DCE时,BP=CE=3,
∴2t=3,
∴t=![]() ,
,
当△ABP≌△CDE时,AP=CE=3,
∴8+6+8﹣2t=3,
∴t=![]() ,
,
即:t=![]() 秒或
秒或![]() 秒时,△ABP和△DCE全等.
秒时,△ABP和△DCE全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商厦进货员预测一种应季衬衫能畅销市场,就用
 万元购进这种衬衫,面市后果然供不应求.商厦又用
万元购进这种衬衫,面市后果然供不应求.商厦又用 万元购进第二批这种衬衫,所购数量是第一批进量的
万元购进第二批这种衬衫,所购数量是第一批进量的 倍,但单价贵了
倍,但单价贵了 元.商厦销售这种衬衫时每件定价
元.商厦销售这种衬衫时每件定价 元,最后剩下
元,最后剩下 件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元?
件按八折销售,很快售完.在这两笔生意中,商厦共盈利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=
 AD时(如图2):
AD时(如图2):∵AP=
 AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,∴S△ABP=
 S△ABD,
S△ABD,∵PD=AD﹣AP=
 AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等∴S△CDP=
 S△CDA,
S△CDA,∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣
 S△ABD﹣
S△ABD﹣ S△CDA,
S△CDA,=S四边形ABCD﹣
 (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣ (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)= S△DBC+
S△DBC+ S△ABC.
S△ABC.(1)当AP=
 AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;(2)当AP=
 AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;(3)一般地,当AP=
 AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;(4)当AP=
 AD(0≤
AD(0≤ ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
-
科目: 来源: 题型:
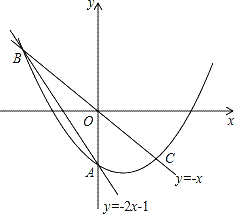
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为原点,直线y=2x﹣1,与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(1)求过A,B,C三点的抛物线的解析式;
(2)P为抛物线上一点,它关于原点的对称点为Q,当四边形PBQC为菱形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
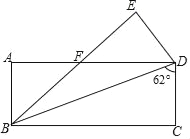
A. 31° B. 28° C. 62° D. 56°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形ABCD中,AE平分
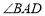 交BC于E,
交BC于E,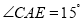 ,则下面的结论:①
,则下面的结论:①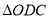 是等边三角形;②
是等边三角形;②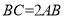 ;③
;③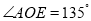 ;④
;④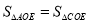 ,其中正确结论有( )
,其中正确结论有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
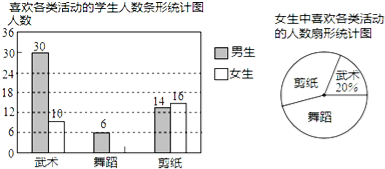
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
相关试题

