【题目】如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为![]() 秒.
秒.
(1)运动_____秒时,CD=3AE.
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=![]() 则∠ADE=_______(用含
则∠ADE=_______(用含![]() 的式子表示)。
的式子表示)。

参考答案:
【答案】(1)3秒;(2)当t=2时,△ABD与△DCE全等;理由见解析;(3)90°-0.5ɑ.
【解析】
(1)依据BD=CE=2t,可得CD=12-2t,AE=8-2t,再根据当DC=3AE时,12-2t =3(8-2t),可得t的值;
(2)当△ABD≌△DCE成立时,AB=CD=8,根据12-2t=8,可得t的值;
(3)依据∠CDE=∠BAD,∠ADE=180°-∠CDE-∠ADB,∠B=∠180°-∠BAD-∠ADB,即可得到∠ADE=∠B,再根据∠BAC=α,AB=AC,即可得出∠ADE.
(1)由题可得,BD=CE=2t,
∴CD=12-2t,AE=8-2t,
∴当DC=3AE时,12-2t =3(8-2t),
解得t=3,
故答案为:3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12-2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°-∠CDE-∠ADB,∠B=∠180°-∠BAD-∠ADB,
∴∠ADE=∠B,
又∵∠BAC=α,AB=AC,
∴∠ADE=∠B=![]() (180°-α)=90°-
(180°-α)=90°-![]() α.
α.
故答案为:90°-![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为 时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为 时,四边形ACFE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
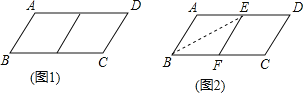
(1)判断与推理:
①邻边长分别为2和3的平行四边形是 阶准菱形;
②小明为了剪去一个菱形,进行了如下操作:如图,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(2)操作、探究与计算:
①已知ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出ABCD是几阶准菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:(1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB
___A1B1;

(2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB___A2B2;
(3)当线段AB垂直于投影面P时,它的正投影是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一角度α后(0°<α<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;
(3)若BC=DE=2,正方形DEFG绕点D逆时针方向旋转角度α (0°<α<360°)过程中,当BG为最小值时,求AF的值.
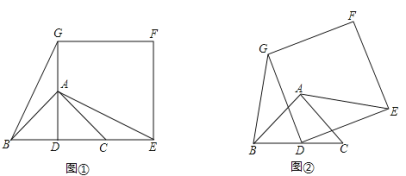
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
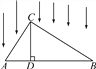
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校墙边有两根木杆.
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
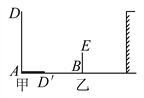
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?
相关试题

