【题目】某校墙边有两根木杆.
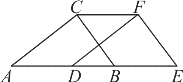
(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出乙木杆的影子吗?(用线段表示影子)
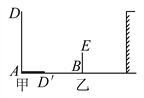
(2)当乙木杆移动到什么位置时,其影子刚好不落在墙上?
(3)在你所画的图中有相似三角形吗?
参考答案:
【答案】(1)画图见解析;(2)见解析;(3)有,△ADD′与△BEE′相似.
【解析】试题分析:(1)连接甲木杆影子的顶端和甲木杆的顶端DD′就是光线的位置,同时太阳光线是平行的,经过点E作DD′的平行线交AB于点E′即可画出乙木杆的影子;
(2)平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE′),直到影子的顶端E′抵达墙脚即可;
(3)利用相似三角形的判定找出相似三角形.
试题解析:
解:(1)如答图1,连接DD′,过E点作直线DD′的平行线,交AD′所在直线于E′,则BE′为乙木杆的影子;

(2)如答图2,平移由乙木杆、乙木杆的影子和太阳光线所构成的图形(即△BEE′),直到影子的顶端E′抵达墙脚;
(3)有,△ADD′与△BEE′相似.
∵DD′∥EE′,
∴∠DD′A=∠EE′B ,
又∵∠DAD′=∠EBE′,
∴△ADD′∽△BEE′(两角对应相等,两三角形相似).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=8,BC=12,点D从B出发以每秒2个单位的速度在线段BC上从过点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为
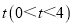 秒.
秒.(1)运动_____秒时,CD=3AE.
(2)运动多少秒时,△ABD≌△DCE能成立,并说明理由;
(3)若△ABD≌△DCE,∠BAC=
 则∠ADE=_______(用含
则∠ADE=_______(用含 的式子表示)。
的式子表示)。
-
科目: 来源: 题型:
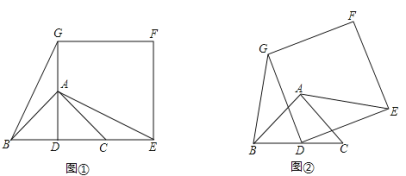
查看答案和解析>>【题目】如图(1),已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的关系(位置关系及数量关系),请直接写出你得到的结论;
(2)将正方形DEFG绕点D逆时针方向旋转一角度α后(0°<α<90°),如图(2),通过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;
(3)若BC=DE=2,正方形DEFG绕点D逆时针方向旋转角度α (0°<α<360°)过程中,当BG为最小值时,求AF的值.
-
科目: 来源: 题型:
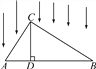
查看答案和解析>>【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,則四辺形ABFD的周长为( )

A. 16cmB. 18cmC. 20cmD. 22cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8cm,DB=2cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
相关试题

