【题目】若数列{an}是正项数列,且 ![]() +
+ ![]() +…+
+…+ ![]() =n2+3n(n∈N*),则
=n2+3n(n∈N*),则 ![]() +
+ ![]() +…+
+…+ ![]() = .
= .
参考答案:
【答案】2n2+6n
【解析】解:令n=1,得 ![]() =4,∴a1=16. 当n≥2时,
=4,∴a1=16. 当n≥2时,![]() +
+ ![]() +…+
+…+ ![]() =(n﹣1)2+3(n﹣1).
=(n﹣1)2+3(n﹣1).
与已知式相减,得![]() =(n2+3n)﹣(n﹣1)2﹣3(n﹣1)=2n+2,
=(n2+3n)﹣(n﹣1)2﹣3(n﹣1)=2n+2,
∴an=4(n+1)2 , n=1时,a1适合an .
∴an=4(n+1)2 ,
∴ ![]() =4n+4,
=4n+4,
∴ ![]() +
+ ![]() +…+
+…+ ![]() =
= ![]() =2n2+6n.
=2n2+6n.
故答案为2n2+6n
根据题意先可求的a1 , 进而根据题设中的数列递推式求得 ![]() +
+ ![]() +…+
+…+ ![]() =(n﹣1)2+3(n﹣1)与已知式相减即可求得数列{an}的通项公式,进而求得数列{
=(n﹣1)2+3(n﹣1)与已知式相减即可求得数列{an}的通项公式,进而求得数列{ ![]() }的通项公式,可知是等差数列,进而根据等差数列的求和公式求得答案.
}的通项公式,可知是等差数列,进而根据等差数列的求和公式求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 ,则满足f(f(m))=3f(m)的实数m的取值范围是( )
,则满足f(f(m))=3f(m)的实数m的取值范围是( )
A.(﹣∞,0)∪{﹣ }
}
B.[0,1]
C.[0,+∞)∪{﹣ }
}
D.[1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输入A的值为2.5,则输出的P值为( )

A.6
B.7
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形△ABC的三边长构成公差为2的等差数列,且最大角的正弦值为
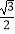 ,则这个三角形的周长为( )
,则这个三角形的周长为( )
A.15
B.18
C.21
D.24 -
科目: 来源: 题型:
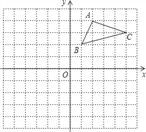
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ,a=2,
,a=2,  ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=
 ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
相关试题

