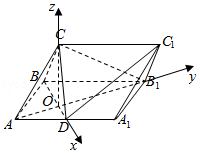
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB= ![]() ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
参考答案:
【答案】
(1)证明:由题意可知,在Rt△ABD中,tan∠ABD= ![]() =
= ![]() ,
,
在Rt△ABB1中,tan∠AB1B= ![]() =
= ![]() .
.
又因为0<∠ABD,∠AB1B ![]() ,所以∠ABD=∠AB1B,
,所以∠ABD=∠AB1B,
所以∠ABD+∠BAB1=∠AB1B+∠BAB1= ![]() ,
,
所以AB1⊥BD.
又CO⊥侧面ABB1A1,且AB1侧面ABB1A1,∴AB1⊥CO.又BD与CO交于点O,所以AB1⊥平面CBD.
又因为BC平面CBD,所以BC⊥AB1.
(2)解:如图所示,以O为原点,分别以OD,OB1,OC所在的直线为x轴,y轴,z轴,建立空间直角坐标系,
则A(0,﹣ ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0,0),C(0,0,
,0,0),C(0,0, ![]() ),
),
B1(0, ![]() ,0),D(
,0),D( ![]() ,0,0).
,0,0).
又因为 ![]() =2
=2 ![]() ,所以C1(
,所以C1( ![]() ,
, ![]() ,
, ![]() ).
).
所以 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ).
).
设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则由  ,得
,得 
令y= ![]() ,则z=﹣
,则z=﹣ ![]() ,x=1,
,x=1, ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() )是平面ABC的一个法向量.
)是平面ABC的一个法向量.
设直线C1D与平面ABC所成的角为α,
则sin α=  =
= ![]() .
.
故直线C1D与平面ABC所成角的正弦值为 ![]() .
.
【解析】(1)推导出∠ABD=∠AB1B,从而∠ABD+∠BAB1=∠AB1B+∠BAB1= ![]() ,进而AB1⊥BD.由线面垂直得AB1⊥CO.从而AB1⊥平面CBD.由此能证明BC⊥AB1 . (2)以O为原点,分别以OD,OB1 , OC所在的直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出直线C1D与平面ABC所成角的正弦值.
,进而AB1⊥BD.由线面垂直得AB1⊥CO.从而AB1⊥平面CBD.由此能证明BC⊥AB1 . (2)以O为原点,分别以OD,OB1 , OC所在的直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出直线C1D与平面ABC所成角的正弦值.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}是正项数列,且
 +
+  +…+
+…+  =n2+3n(n∈N*),则
=n2+3n(n∈N*),则  +
+  +…+
+…+  = .
= . -
科目: 来源: 题型:
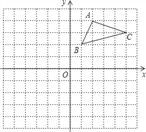
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ,a=2,
,a=2,  ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组
频数
频率
[10,15)
10
0.25
[15,20)
25
n
[20,25)
m
p
[25,30)
2
0.05
合计
M
1

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1:
 的长轴长是4,椭圆C2:
的长轴长是4,椭圆C2: 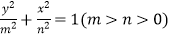 短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点,
短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点, 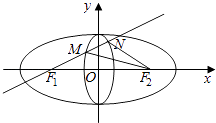
(Ⅰ)求椭圆C1 , C2的方程;
(Ⅱ)过F1的直线交椭圆C2于点M,N,求△F2MN面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+x2﹣2ax+1(a为常数).
(1)讨论函数f(x)的单调性;
(2)若对任意的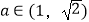 ,都存在x0∈(0,1]使得不等式
,都存在x0∈(0,1]使得不等式  成立,求实数m的取值范围.
成立,求实数m的取值范围.
相关试题

