【题目】已知函数 ![]() . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ![]() ,a=2,
,a=2, ![]() ,求△ABC的面积.
,求△ABC的面积.
参考答案:
【答案】解:(Ⅰ) ![]() =sin2xcos
=sin2xcos ![]() +cos2xsin
+cos2xsin ![]() +cos2x =
+cos2x = ![]() sin2x+
sin2x+ ![]() cos2x=
cos2x= ![]() (
( ![]() sin2x+
sin2x+ ![]() cos2x)=
cos2x)= ![]() sin(2x+
sin(2x+ ![]() ).
).
令 2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,求得 kπ﹣
,k∈z,求得 kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
函数f(x)的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈z.
],k∈z.
(Ⅱ)由已知 ![]() ,可得 sin(2A+
,可得 sin(2A+ ![]() )=
)= ![]() ,
,
因为A为△ABC内角,由题意知0<A<π,所以 ![]() <2A+
<2A+ ![]() <
< ![]() ,
,
因此,2A+ ![]() =
= ![]() ,解得A=
,解得A= ![]() .
.
由正弦定理 ![]() ,得b=
,得b= ![]() ,…
,…
由A= ![]() ,由B=
,由B= ![]() ,可得 sinC=
,可得 sinC= ![]() ,…
,…
∴S= ![]() absinC=
absinC= ![]() =
= ![]() .
.
【解析】(Ⅰ)利用两角和差的正弦公化简函数的解析式为 ![]() sin(2x+
sin(2x+ ![]() ),令 2kπ﹣
),令 2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈z,求得x的范围,即可求得f(x)的单调递增区间.(Ⅱ)由已知
,k∈z,求得x的范围,即可求得f(x)的单调递增区间.(Ⅱ)由已知 ![]() ,可得 sin(2A+
,可得 sin(2A+ ![]() )=
)= ![]() ,求得A=
,求得A= ![]() ,再利用正弦定理求得b的值,由三角形内角和公式求得C的值,再由 S=
,再利用正弦定理求得b的值,由三角形内角和公式求得C的值,再由 S= ![]() absinC,运算求得结果.
absinC,运算求得结果.
【考点精析】通过灵活运用两角和与差的正弦公式和正弦函数的单调性,掌握两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数即可以解答此题.
上是减函数即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形△ABC的三边长构成公差为2的等差数列,且最大角的正弦值为
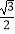 ,则这个三角形的周长为( )
,则这个三角形的周长为( )
A.15
B.18
C.21
D.24 -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}是正项数列,且
 +
+  +…+
+…+  =n2+3n(n∈N*),则
=n2+3n(n∈N*),则  +
+  +…+
+…+  = .
= . -
科目: 来源: 题型:
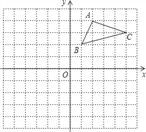
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=
 ,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:CD⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组
频数
频率
[10,15)
10
0.25
[15,20)
25
n
[20,25)
m
p
[25,30)
2
0.05
合计
M
1

(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的. 如图,椭圆C1与椭圆C2是相似的两个椭圆,并且相交于上下两个顶点.椭圆C1:
 的长轴长是4,椭圆C2:
的长轴长是4,椭圆C2: 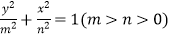 短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点,
短轴长是1,点F1 , F2分别是椭圆C1的左焦点与右焦点, 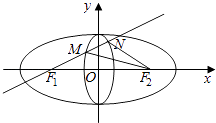
(Ⅰ)求椭圆C1 , C2的方程;
(Ⅱ)过F1的直线交椭圆C2于点M,N,求△F2MN面积的最大值.
相关试题

