【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
参考答案:
【答案】(1) 商家一次购买这种产品50件时,销售单价恰好为2600元;(2) 当0≤x≤10时,y=600x;当10<x≤50时,y =-10x2+700x;当x>50时,y =200x;(3) 公司应将最低销售单价调整为2750元.
【解析】
试题分析: (1)根据:原定售价-超过10件而降低的价格=实际售价,列方程可得;
(2)由销售单价均不低于2600元求出x的取值范围,根据实际售价不同分0≤x≤10、10<x≤50、x>50三种情况列出函数关系式;
(3)根据题意,此时情形满足10<x≤50时,y与x的函数关系,根据二次函数性质可求得最值并确定此时x的值.
试题解析:(1)设件数为x,根据题意,
得:3000-10(x-10)=2600,
解得:x=50,
答:商家一次购买这种产品50件时,销售单价恰好为2600元;
(2)由题意,得:3000-10(x-10)≥2600,
解得:x≤50,
当0≤x≤10时,y=(3000-2400)x=600x;
当10<x≤50时,y=[3000-2400-10(x-10)]x=-10x2+700x;
当x>50时,y=(2600-2400)x=200x;
(3)由y=-10x2+700x可知抛物线开口向下,
当x=-![]() =35时,利润y有最大值,
=35时,利润y有最大值,
此时销售单价为;3000-10×(35-10)=2750(元),
答:公司应将最低销售单价调整为2750元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ.给出如下结论:
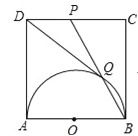
①DQ与半圆O相切;②
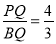 ;③∠ADQ=2∠CBP;④cos∠CDQ=
;③∠ADQ=2∠CBP;④cos∠CDQ=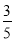 .其中正确的是 (请将正确结论的序号填在横线上).
.其中正确的是 (请将正确结论的序号填在横线上). -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:|x-1|+|x-3|>4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 要了解我市九年级学生的身高,应采用普查的方式;
B. 若甲队成绩的方差为5,乙队成绩的方差为3,则甲队成绩不如乙队成绩稳定;
C. 如果明天下雨的概率是99%,那么明天一定会下雨;
D. 一组数据4,6,7,6,7,8,9的中位数和众数都是6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
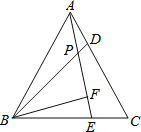
A.2
B.3
C.1
D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=x+6与反比例函数y2=
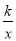 (x<0)的图象相交于点A、B,其中点A的坐标是(-2,4).
(x<0)的图象相交于点A、B,其中点A的坐标是(-2,4).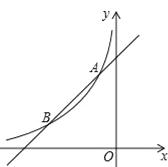
(1)求反比例函数的解析式和点B的坐标;
(2)观察图象,比较当x<0时,y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A.5个
B.4个
C.3个
D.2个
相关试题

