【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A.5个
B.4个
C.3个
D.2个
参考答案:
【答案】A
【解析】
试题分析:根据已知条件和等腰三角形的判定定理,对图中的三角形进行分析,即可得出答案.
解:共有5个.
(1)∵AB=AC
∴△ABC是等腰三角形;
(2)∵BD、CE分别是∠ABC、∠BCD的角平分线
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
∵△ABC是等腰三角形,
∴∠EBC=∠ECB,
∴△BCE是等腰三角形;
(3)∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=![]() (180°﹣36°)=72°,
(180°﹣36°)=72°,
又BD是∠ABC的角平分线,
∴∠ABD=![]() ∠ABC=36°=∠A,
∠ABC=36°=∠A,
∴△ABD是等腰三角形;
同理可证△CDE和△BCD是等腰三角形.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技开发公司研制出一种新型产品,每件产品的成本为2400元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获的利润最大,公司应将最低销售单价调整为多少元(其它销售条件不变)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
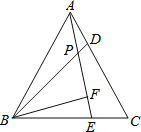
A.2
B.3
C.1
D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=x+6与反比例函数y2=
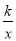 (x<0)的图象相交于点A、B,其中点A的坐标是(-2,4).
(x<0)的图象相交于点A、B,其中点A的坐标是(-2,4).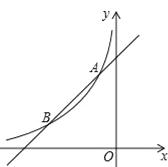
(1)求反比例函数的解析式和点B的坐标;
(2)观察图象,比较当x<0时,y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中错误的是( )
A. 平行四边形的对角线互相平分 B. 菱形的对角线互相垂直
C. 同旁内角互补 D. 矩形的对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】据2010年第六次全国人口普查公布的数据显示,全桂林市总人口为498.84万人,那么用科学记数法表示为( )人.
A. 4.98846 B. 4.9884×106 C. 4.9884×107 D. 4.9884×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形的重心在它的一条高上,则这个三角形一定是( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
相关试题

