Question

【题目】如图，在正方形ABCD中，以AB为直径作半圆，点P是CD中点，BP与半圆交于点Q，连结DQ．给出如下结论：

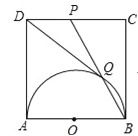
①DQ与半圆O相切；②；③∠ADQ=2∠CBP；④cos∠CDQ=．其中正确的是 （请将正确结论的序号填在横线上）．

Answer 1

【答案】①③

【解析】

试题解析：①如图1

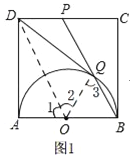
连接DO，OQ，在正方形ABCD中，AB∥CD，AB═CD，

∵P是CD中点，O是AB中点，

∴DP∥OB，DP═OB，

∴四边形OBDP是平行四边形，

∴OD∥BP，

∴∠1=∠OBQ，∠2=∠3，

又∵OQ=OB，

∴∠3=∠OBQ，

∴∠1=∠2，

在△AOD和△QOD中，

，

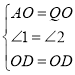∴△AOD≌△QOD，

∴∠OQD=∠A=90°，

∴DQ与半圆O相切，

①正确；

②如图2

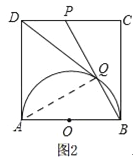
连接AQ，可得：∠AQB=90°，

在正方形ABCD中，AB∥CD，

∴∠ABQ=∠BPC，

设正方形边长为x，则CP=x，

由勾股定理可求：BP=，

∴cos∠BPC=，cos∠ABQ=，

∴=，又AB=x，

可求，BQ=x，

PQ=x，

∴，

②不对；

③如图3

连接AQ，OQ，

由①知，∠OQD=90°，又∠OAD=90°，可求∠ADQ+∠AOQ=180°，

∵∠3+∠AOQ=180°，

∴∠3=∠ADQ，

由②知，∠1+∠4=90°，

又∠4+∠CBP=90°，

∴∠CBP=∠1，

∵OA=OQ，

∴∠1=∠2，

又∵∠3=∠1+∠2，

∴∠3=2∠CBP，

∴∠ADQ=2∠CBP，

故③正确；

④如图4，

过点Q作QH⊥CD，

易证QH∥BC，

设正方形边长为x，由②知：PQ=x，cos∠BPC=，

可求：PH=x，HQ=x，

∴DH=DP+PH=x，

由勾股定理可求：DQ=x，

∴cos∠CDQ=，

故④不正确．

综上所述：正确的有①③．