【题目】如图1,平行四边形ABCD在平面直角坐标系中,A、B(点A在点B的左侧)两点的横坐标是方程![]() 的两个根,点D在y轴上其中
的两个根,点D在y轴上其中![]() .
.

(1)求平行四边形ABCD的面积;
(2)若P是第一象限位于直线BD上方的一点,过P作![]() 于E,过E作
于E,过E作![]() 轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是
轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是![]() ;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求
;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求![]() 的最小值,此时y轴上有一个动点G,当
的最小值,此时y轴上有一个动点G,当![]() 最大时,求G点坐标;
最大时,求G点坐标;
(3)在(2)的情况下,将△AOD绕O点逆时针旋转60°后得到![]() 如图2,将线段
如图2,将线段![]() 沿着x轴平移,记平移过程中的线段
沿着x轴平移,记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点S,使得以点
,在平面直角坐标系中是否存在点S,使得以点![]() ,
,![]() ,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)S平行四边形ABCD=48;(2)G(0,![]() ),见解析;(3)满足条件的点S的坐标为
),见解析;(3)满足条件的点S的坐标为![]() 或
或![]() 或
或![]() ,见解析.
,见解析.
【解析】
(1)解方程求出A,B两点坐标,在Rt△AOD中,求出OD即可解决问题.
(2)首先证明△EHB也是等腰直角三角形,以HE,HB为边构造正方形EHBJ,连接JN,延长JE交OD于Q,作MT⊥OD于T,连接JT.在Rt△DMT中,易知MT=![]() DM,根据对称性可知:NH=NJ,推出HN+MM-
DM,根据对称性可知:NH=NJ,推出HN+MM-![]() DM=NJ+MN-MT≤JT,推出当JT最小时,HN+MM-
DM=NJ+MN-MT≤JT,推出当JT最小时,HN+MM-![]() DM的值最小.如图2中当点M在JQ的延长线上时,HN+MM-
DM的值最小.如图2中当点M在JQ的延长线上时,HN+MM-![]() DM的值最小,此时M(-
DM的值最小,此时M(-![]() ,5),作点M关于y轴对称点M′,连接CM′,延长CM′交y轴于点G,此时|CG-MG|最大,求出直线CM′的解析式即可解决问题.
,5),作点M关于y轴对称点M′,连接CM′,延长CM′交y轴于点G,此时|CG-MG|最大,求出直线CM′的解析式即可解决问题.
(3)分五种情形分别画出图形,利用菱形的性质,中点坐标公式等知识一一求解即可.
解:(1)由![]() 得到x=-2或6;
得到x=-2或6;
∴A(-2,0),B(6,0);
在Rt△ADO中,∵∠AOD=90°,AD=2![]() ,OA=2;
,OA=2;
![]() ,
,
∵OB=6,
∴OD=OB=6,
∴△BOD是等腰直角三角形,
∴S平行四边形ABCD=ABOD=8×6=48;
(2)如图1中,
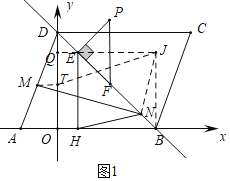
∵EH⊥OB,
∴∠EHB=90°,
∵△BOD是等腰直角三角形,
∴∠EBH=45°,
∴△EHB也是等腰直角三角形,
以HE,HB为边构造正方形EHBJ,连接JN,延长JE交OD于Q,作MT⊥OD于T,连接JT,在Rt△DMT中,易知MT=![]() DM,
DM,
∵四边形EHBJ是正方形,
根据对称性可知:NH=NJ,
∴HN+MM-![]() DM=NJ+MN-MT≤JT,
DM=NJ+MN-MT≤JT,
∴当JT最小时,HN+MM-![]() DM的值最小,
DM的值最小,
∵JT≤JQ,
∴JT≤OB=6,
∴HN+MM-![]() DM的最小值为6.
DM的最小值为6.
如图2中,∵PF∥y轴,
∴∠PFE=∠ODB=45°,
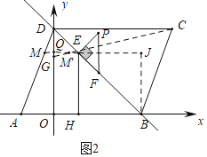
∴△PEF是等腰直角三角形,设PE=EF=a,则PF=![]() a,
a,
由题意2a+![]() a=4+4
a=4+4![]() ,
,
∴a=2![]() ,
,
∵FB=FD,
∴F(3,3),
∴E(1,5),
∴当点M在JQ的延长线上时,HN+MM-![]() DM的值最小,此时M(-
DM的值最小,此时M(-![]() ,5),作点M关于y轴对称点M′,连接CM′,延长CM′交y轴于点G,此时|CG-MG|最大,
,5),作点M关于y轴对称点M′,连接CM′,延长CM′交y轴于点G,此时|CG-MG|最大,
∵C(8,6),M′(![]() ,5),
,5),
∴直线CM′的解析式为![]() ,
,
∴G(0,![]() );
);
(3)存在.设菱形的对角线的交点为J.
①如图3-1中,当O′D″是对角线时,设ES交x轴于T.
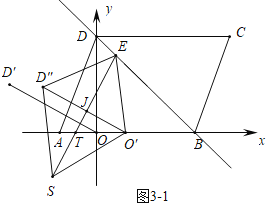
∵四边形EO′SD″是菱形,
∴ES⊥O′D″,
∴直线ES的解析式为![]() ,
,
∴T![]() ,
,
在Rt△JTO′中,易知O′J=3,∠TO′J=30°,
∴O′T=2![]() ,
,
![]() ,
,
![]()
∵JE=JS,
∴可得S![]() ,
,
②如图3-2中,当EO′=O′D″=6时,可得四边形SEO′D″是菱形,设O′(m,0).
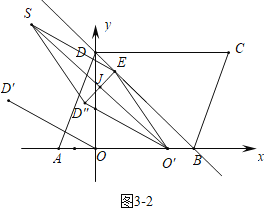
则有:(m-1)2+52=36,
∴m=1+![]() 或1-
或1-![]() ,
,
∴O′(1+![]() ,0)或(1-
,0)或(1-![]() ,0)(如图3-3中),
,0)(如图3-3中),
∴D″(1+![]() -3
-3![]() ,3),
,3),
∴![]() ;
;
∵JS=JO′,
![]() ,
,
③如图3-3中,当EO′=O′D″时,由②可知O′(1-![]() ,0).同法可得
,0).同法可得![]()
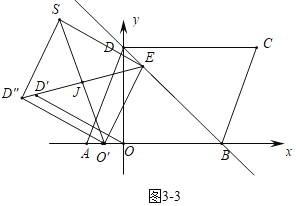
④如图3-4中,当ED″=D″O′=6时,可得四边形ESO′D″是菱形.
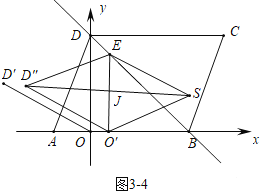
设D″(m,3),则(m-1)2+22=36,
∴m=1+4![]() (图5中情形),或m=1-4
(图5中情形),或m=1-4![]() ,
,
![]() ,
,
![]() ,
,
∵JD″=JS,
∴可得S(1+3![]() ,2),
,2),
⑤如图3-5中,当D″E=D″O时,由④可知D″(1+4![]() ,3),
,3),
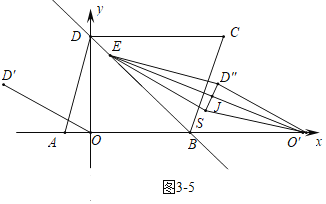
![]() ,
,
![]() ,
,
∵JD″=JS,
∴可得S(1+3![]() ,2),
,2),
综上所述,满足条件的点S的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为37°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB和楼房MN的高度.
(
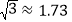 ,
,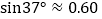 ,
,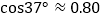 ,
,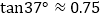 ,结果精确到0.1m)
,结果精确到0.1m)
-
科目: 来源: 题型:
查看答案和解析>>【题目】淘宝11.11购物节期间,小垣妈妈在网上某品牌服装店按标价八折拍到一件学生外套,用支付宝支付了120元.爱思考的小垣进行了下列研究:
(1)该学生外套在网上的标价是 元.
(2)妈妈告诉小垣她在网上买到的学生外套商家可以获得20%的利润.根据妈妈的说法,一件学生外套的进价是多少元?
(3)小垣搜索发现标价相同的同款学生外套在网上另一店铺打折优惠,并规定订单金额满200元,可以使用30元店铺优惠券.她告诉妈妈如果一次购买2件只需要支付225元,那么该网店同款学生外套打几折进行优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练,机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动,已知AD=6个单位长度,机器人的速度为1个单位长度/s且其移动至拐角处调整方向所需时间忽略不计.设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)图②中函数图象与纵轴的交点的纵坐标
 在图①中表示一条线段的长,请在图①中画出这条线段.
在图①中表示一条线段的长,请在图①中画出这条线段.(2)求图②中a的值;
(3)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在二次函数y=ax2+bx+c的图象中,你认为其中正确的是( )
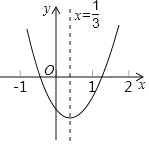
A. a>0 B. c>0
C. b2﹣4ac<0 D. 一元二次方程ax2+bx+c=0有两个相等实根
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
幻方的历史很悠久,传说中最早出现在夏禹时代的“洛书”,用今天的数学符号翻译出来,就是一个三阶幻方,即将若干个数组成一个正方形数阵,任意一行、一列及对角线上的数字之和都相等.如图1,就是一个三阶幻方,由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的矩阵(如图),其对角线、横行、纵向的和都为15.
(1)探究:研究发现三阶幻方中间的数字与9个数的和有确定的数量关系.如果设数字连续性三阶幻方中间的数字是a,则幻方中9个数字之和是 (用含a的字母代数式表示)
(2)应用:请你选取一组数据构造一个三阶幻方,填入到如图2的3×3方格中,使得每行、每列、每条对角线上的三个数之和都等于21;


(3)拓展:
数阵是由幻方演化出来的另一种数字图.将连续的奇数1,3,5,7,9…排列成数阵(如图3),用十字框随机框出5个数,十字框中的五数之和能等于2020吗?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是小明某一周的收支情况,规定收入为正,支出为负.(单位:元)
周一
周二
周三
周四
周五
周六
周日
15
12
0
20
15
10
14
8
12
19
10
9
11
8
(1)小明哪天的收入小于支出?答:
(2)小明这一周的平均支出是多少?
(3)小明这一周共有多少节余?
相关试题

