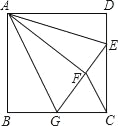
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=![]() .其中正确的是( )
.其中正确的是( )
A. ①③ B. ②③ C. ①④ D. ②④
参考答案:
【答案】C
【解析】解:∵正方形ABCD中,AB=3,CD=3DE,∴DE=![]() ×3=1,CE=3﹣1=2.∵△ADE沿AE对折至△AFE,∴AD=AF,EF=DE=1,∠AFE=∠D=90°,∴AB=AF=AD.在Rt△ABG和Rt△AFG中,
×3=1,CE=3﹣1=2.∵△ADE沿AE对折至△AFE,∴AD=AF,EF=DE=1,∠AFE=∠D=90°,∴AB=AF=AD.在Rt△ABG和Rt△AFG中,![]() ,∴Rt△ABG≌Rt△AFG(HL),∴BG=FG,设BG=FG=x,则EG=EF+FG=1+x,CG=3﹣x.在Rt△CEG中,EG2=CG2+CE2,即(1+x)2=(3﹣x)2+22,解得,x=
,∴Rt△ABG≌Rt△AFG(HL),∴BG=FG,设BG=FG=x,则EG=EF+FG=1+x,CG=3﹣x.在Rt△CEG中,EG2=CG2+CE2,即(1+x)2=(3﹣x)2+22,解得,x=![]() ,∴CG=3﹣
,∴CG=3﹣![]() =
=![]() ,∴BG=CG=
,∴BG=CG=![]() ,即点G是BC中点,故①正确;
,即点G是BC中点,故①正确;
∵tan∠AGB=![]() =2,∴∠AGB≠60°,∴∠CGF≠180°﹣60°×2≠60°.又∵BG=CG=FG,∴△CGF不是等边三角形,∴FG≠FC,故②错误;
=2,∴∠AGB≠60°,∴∠CGF≠180°﹣60°×2≠60°.又∵BG=CG=FG,∴△CGF不是等边三角形,∴FG≠FC,故②错误;
由(1)知Rt△ABG≌Rt△AFG,∴∠AGB=∠AGF=![]() ∠BGF,根据三角形的外角性质,∠GCF+∠GFC=∠AGB+∠AGF,∴∠GCF=∠GFC=∠AGB.∵AD∥BC,∴∠AGB=∠GAD,∴与∠AGB相等的角有4个,故③错误;
∠BGF,根据三角形的外角性质,∠GCF+∠GFC=∠AGB+∠AGF,∴∠GCF=∠GFC=∠AGB.∵AD∥BC,∴∠AGB=∠GAD,∴与∠AGB相等的角有4个,故③错误;
△CGE的面积=![]() CGCE=
CGCE=![]() ×
×![]() ×2=
×2=![]() .∵EF:FG=1:
.∵EF:FG=1:![]() =2:3,∴S△
=2:3,∴S△![]() ×
×![]() =
=![]() ,故④正确.
,故④正确.
综上所述:正确的结论有①④.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证:BD
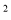 +CD
+CD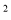 =2AD
=2AD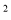 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求
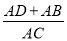 的值。.
的值。.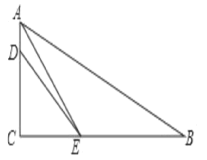
-
科目: 来源: 题型:
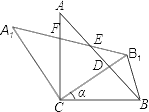
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90,AC=BC,将△ABC绕点C逆时针旋转α角(0<α<90)得到△A1B1C,连结BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F,
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC与△A1B1C全等除外);
(2)当△BB1D是等腰三角形时,求α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市高中招生体育考试前教育部门为了解全市九年级男生考试项目的选择情况(每人限选一项),对全市部分九年级男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)将上面的条形统计图补充完整;
(2)假定全市九年级毕业学生中有5500名男生,试估计全市九年级男生中选“50米跑”的人数有多少人?
(3)甲、乙两名九年级男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球和立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
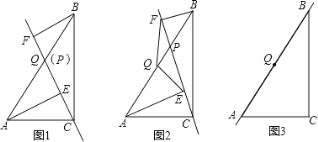
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
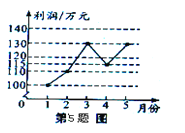
A. 1~2月份利润的增长快于2~3月份分利润的增长
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~5月份利润的的众数是130万元
D. 1~5月份利润的中位数为120万元
相关试题

