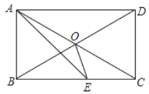
【题目】如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠OAE=15°,则∠AEO的度数为__________.
参考答案:
【答案】![]()
【解析】
根据矩形性质和角平分线的定义求证△ABO为等边三角形,从而得到∠ABO=60°,然后根据平行线的性质得出∠AEB=∠EAD=45°,从而得出BE=AB=BO,然后利用等腰三角形等边对等角的性质求得∠BEO=(180°-30°)÷2=75°,从而使问题得解.
解:∵四边形ABCD是矩形
∴OA=OB,∠BAD=∠ABC=90°,
又∵AE平分∠BAD
∴∠BAE=45°,
∴∠BAO=∠BAE +∠EAC =60°
∴△ABO为等边三角形
∴∠AOB=∠ABO=60°,
∴∠OBE=∠ABC-∠ABO=30°
∵AD//BC
∴∠AEB=∠EAD=45°
∴∠BAE=∠AEB
∴BE=AB=BO
∴∠BEO=(180°-30°)÷2=75°
∴∠AEO=∠BEO-∠AEB=30°
故答案为:30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n
100
200
300
500
800
1000
摸到黑棋的次数m
24
51
76
b
201
250
摸到黑棋的频率
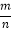 (精确到0.001)
(精确到0.001)0.240
a
0.253
0.248
0.251
0.250
(1)填空:a= ,b= ;
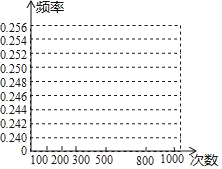
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)
-
科目: 来源: 题型:
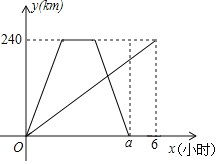
查看答案和解析>>【题目】A、B两地相距240km,甲骑摩托车由A地驶往B地,乙驾驶汽车由B地驶往A地,甲乙两人同时出发,乙达到A地停留1小时后,按原路原速返回B地,甲比乙晚1小时到达B地,甲、乙两人行驶过程中均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.
(1)在上述变化过程中,自变量是______,因变量是______;
(2)a的值为______;
(3)甲到达B地共需______小时;甲骑摩托车的速度是______km/h;
(4)乙驾驶汽车的速度是多少km/h?
-
科目: 来源: 题型:
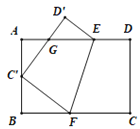
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,这些球除颜色外其他都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)求从袋中摸出一个球不是红球的概率;
(3)现在从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,若从袋中摸出一个球是黄球的概率为
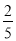 ,则取出了多少个黑球?
,则取出了多少个黑球? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形纸片ABC中,AD⊥BC与点D,BC=2,AD=
 ,沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形中较长对角线的长为__________.
,沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形中较长对角线的长为__________.
相关试题

