【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

参考答案:
【答案】(1)证明见解析;(2)∠BOC=110°.
【解析】试题分析:(1)根据等腰三角形的性质可得:∠ABC=∠ACB,由同角的余角相等可得:∠ABD=∠ACE,进而推出∠OBC=∠OCB解答即可;
(2)容易得而出∠ABC=∠ACB=55°,进而推出∠A=70°,再根据∠BOC=∠EOD=360°-∠A-∠ADB-∠AEC解答即可.
试题解析:(1)证明:∵AB=AC ,∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°.∴△BEC≌△CDB.∴∠DBC=∠ECB,BE=CD.
在△BOE和△COD中,
∵∠BOE=∠COD,BE=CD,∠BEC=∠BDE=90°.
∴△BOE≌△COD,∴OB=OC;
(2)∵∠ABC=55°,AB=AC,∴∠A=180°﹣2×55°=70°,
∴∠DOE+∠A=180°.∴∠BOC=∠DOE=180°﹣70°=110°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我市参加中考的15 000名学生的视力情况,抽查了1 000名学生的视力进行统计分析,下面四个判断正确的是( )
A. 15000名学生是总体
B. 1000名学生的视力是总体的一个样本
C. 每名学生是总体的一个个体
D. 以上调查是普查
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=( )
A. 2B. -2C. 4D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知BM、CN分别是△
 的两个外角的角平分线,
的两个外角的角平分线,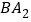 、
、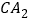 分别是
分别是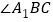 和
和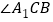 的角平分线,如图①;
的角平分线,如图①;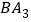 、
、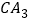 分别是
分别是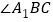 和
和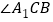 的三等分线(即
的三等分线(即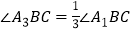 ,
,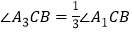 ),如图②;依此画图,
),如图②;依此画图,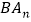 、
、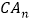 分别是
分别是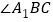 和
和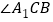 的n等分线(即
的n等分线(即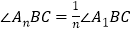 ,
, ),
),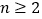 ,且
,且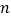 为整数.
为整数.(1)若
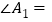
 ,求
,求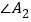 的度数;
的度数;(2)设
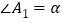 ,请用
,请用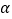 和n的代数式表示
和n的代数式表示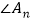 的大小,并写出表示的过程;
的大小,并写出表示的过程;(3)当
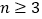 时,请直接写出
时,请直接写出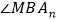 +
+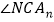 与
与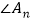 的数量关系.
的数量关系.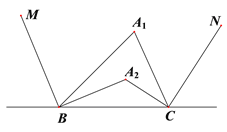

图① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(x,y),且xy>0,x+y<0,则点P在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程3x2-5x+1=0的根的情况是
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果用(7,1)表示七年级一班,那么八年级四班可表示成 .
相关试题

