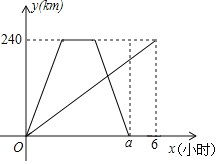
【题目】A、B两地相距240km,甲骑摩托车由A地驶往B地,乙驾驶汽车由B地驶往A地,甲乙两人同时出发,乙达到A地停留1小时后,按原路原速返回B地,甲比乙晚1小时到达B地,甲、乙两人行驶过程中均匀速行驶,甲乙两人离各自出发点的路程y(km)与乙所用时间x(h)的关系如图,结合图象回答下列问题.
(1)在上述变化过程中,自变量是______,因变量是______;
(2)a的值为______;
(3)甲到达B地共需______小时;甲骑摩托车的速度是______km/h;
(4)乙驾驶汽车的速度是多少km/h?
参考答案:
【答案】(1)乙所用的时间x(h);甲乙两人离各自出发点的路程y(km)(2)5(3)6(4)![]() km/h
km/h
【解析】
(1)根据函数图象和函数中的概念解答即可;
(2)利用甲比乙晚1小时到达B地得出a的值即可;
(3)根据图象得出甲到达B地的时间和速度即可;
(4)利用函数图象得出乙驾驶汽车的时间,进而得出速度.
(1)自变量是乙所用的时间x(h),因变量是甲乙两人离各自出发点的路程y(km);
故答案为:乙所用的时间x(h),甲乙两人离各自出发点的路程y(km);
(2)因为甲比乙晚1小时到达B地,所用a=6-1=5;
故答案为:5;
(3)甲到达B地共需6小时,甲骑摩托车的速度是![]() km/h;
km/h;
故答案为:6;40;
(4)由题意可知,乙驾驶汽车行驶的时间为5-1=4(h),
乙驾驶汽车的速度是:![]() (km/h).
(km/h).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABDC中,AB=6,E在CD上,DE=2,将△ADE沿AE折叠至△AFE,延长EF交BC于G,连AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④
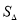 FCG=3,其中正确的有( ).
FCG=3,其中正确的有( ).
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为
 .
.(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
-
科目: 来源: 题型:
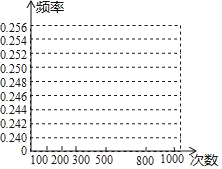
查看答案和解析>>【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n
100
200
300
500
800
1000
摸到黑棋的次数m
24
51
76
b
201
250
摸到黑棋的频率
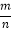 (精确到0.001)
(精确到0.001)0.240
a
0.253
0.248
0.251
0.250
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)
-
科目: 来源: 题型:
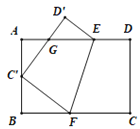
查看答案和解析>>【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
-
科目: 来源: 题型:
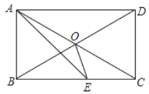
查看答案和解析>>【题目】如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠OAE=15°,则∠AEO的度数为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

相关试题

