【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,动点
,动点![]() 从点
从点![]() 沿
沿![]() 以每秒
以每秒![]() 个单位的速度运动;动点
个单位的速度运动;动点![]() 从点
从点![]() 沿
沿![]() 以每秒
以每秒![]() 个单位的速度运动.
个单位的速度运动.![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() 秒.
秒.
(1)在![]() 时,
时,![]() 点坐标 ,
点坐标 ,![]() 点坐标 ;
点坐标 ;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形?
是矩形?
(3)运动过程中,四边形![]() 能否为菱形?若能,求出
能否为菱形?若能,求出![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
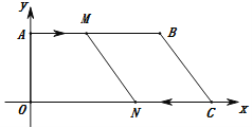
参考答案:
【答案】(1)M(3,8) N(15,0) ;(2)t=7 ;(3)能,t=5 .
【解析】
(1)根据点B、C的坐标求出AB、OA、OC,然后根据路程=速度×时间求出AM、CN,再求出ON,然后写出点M、N的坐标即可;
(2)根据有一个角是直角的平行四边形是矩形,当AM=ON时,四边形OAMN是矩形,然后列出方程求解即可;
(3)先求出四边形MNCB是平行四边形的t值,并求出CN的长度,然后过点B作BC⊥OC于D,得到四边形OABD是矩形,根据矩形的对边相等可得OD=AB,BD=OA,然后求出CD,再利用勾股定理列式求出BC,然后根据邻边相等的平行四边形是菱形进行验证.
解:(1)∵B(15,8),C(21,0),
∴AB=15,OA=8,
OC=21,
当t=3时,AM=1×3=3,
CN=2×3=6,
∴ON=OC-CN=21-6=15,
∴点M(3,8),N(15,0);
故答案为:(3,8);(15,0);
(2)当四边形OAMN是矩形时,AM=ON,
∴t=21-2t,
解得t=7秒,
故t=7秒时,四边形OAMN是矩形;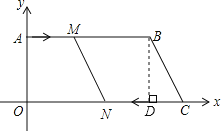
(3)存在t=5秒时,四边形MNCB为菱形.
理由如下:四边形MNCB是平行四边形时,BM=CN,
∴15-t=2t,
解得:t=5秒,
此时CN=5×2=10,
过点B作BD⊥OC于D,则四边形OABD是矩形,
∴OD=AB=15,BD=OA=8,
CD=OC-OD=21-15=6,
在Rt△BCD中,BC=![]() =10,
=10,
∴BC=CN,
∴平行四边形MNCB是菱形,
故,存在t=5秒时,四边形MNCB能否为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中
 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:(1)表示乙离开A地的距离与时间关系的图像是________(填
 );
);甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, .
.
(1)试说明
 成立的理由.(完成下面的填空)
成立的理由.(完成下面的填空)证明:
 ,
,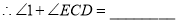 ,(________________)
,(________________)又
 ,(已知)
,(已知) ,(________________)
,(________________) .(________________)
.(________________)(2)若
 平分
平分 ,
, 平分
平分 ,且
,且 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径作⊙O,过点A作⊙O的切线AC,连结BC,交⊙O于点D,点E是BC边的中点,连结AE.
(1)求证:∠AEB=2∠C;
(2)若AB=6,
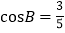 ,求DE的长.
,求DE的长.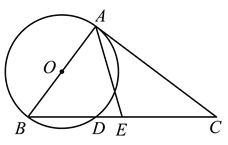
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个口袋中有4个完全相同的小球,把它们分别标号1、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜。否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂生产一种餐桌和椅子,餐桌每张定价为
 元,椅子每把定价为
元,椅子每把定价为 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:每买一张餐桌就赠送一把椅子;
方案二:餐桌和椅子都按定价的
 付款.
付款.某餐厅计划添置
 张餐桌和
张餐桌和 把椅子.
把椅子.(1)若
 ,请用含
,请用含 的代数式分别把两种方案的费用表示出来.
的代数式分别把两种方案的费用表示出来.(2)已知
 ,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案.
,如果两种方案可以同时使用,请帮助餐厅设计一种最省钱的方案. -
科目: 来源: 题型:
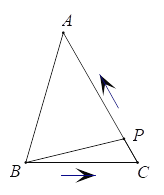
查看答案和解析>>【题目】如图,在△ABC中,∠C=60°,BC=3厘米,AC=4厘米,点P从点B出发,沿B→C→A以每秒1厘米的速度匀速运动到点A.设点P的运动时间为x秒,B、P两点间的距离为y厘米.
小新根据学习函数的经验,对函数
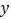 随自变量
随自变量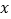 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.下面是小新的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x(s)
0
1
2
3
4
5
6
7
y(cm)
0
1.0
2.0
3.0
2.7
2.7
m
3.6
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:在曲线部分的最低点时,在△ABC中画出点P所在的位置.
相关试题

