【题目】若一组数据![]() ,
,![]() ,
,![]() 的平均数为4,方差为3,那么数据
的平均数为4,方差为3,那么数据![]() ,
,![]() ,
,![]() 的平均数和方差分别是( )
的平均数和方差分别是( )
A. 4, 3 B. 6![]() 3 C. 3
3 C. 3![]() 4 D. 6
4 D. 6![]() 5
5
参考答案:
【答案】B
【解析】根据数据a1,a2,a3的平均数为4可知![]() (a1+a2+a3)=4,据此可得出
(a1+a2+a3)=4,据此可得出![]() (a1+2+a2+2+a3+2)的值;再由方差为3可得出数据a1+2,a2+2,a3+2的方差.
(a1+2+a2+2+a3+2)的值;再由方差为3可得出数据a1+2,a2+2,a3+2的方差.
∵数据a1,a2,a3的平均数为4,
∴![]() (a1+a2+a3)=4,
(a1+a2+a3)=4,
∴![]() (a1+2+a2+2+a3+2)=
(a1+2+a2+2+a3+2)=![]() (a1+a2+a3)+2=4+2=6,
(a1+a2+a3)+2=4+2=6,
∴数据a1+2,a2+2,a3+2的平均数是6;
∵数据a1,a2,a3的方差为3,
∴![]() [(a1-4)2+(a2-4)2+(a3-4)2]=3,
[(a1-4)2+(a2-4)2+(a3-4)2]=3,
∴a1+2,a2+2,a3+2的方差为:![]() [(a1+2-6)2+(a2+2-6)2+(a3+2-6)2]
[(a1+2-6)2+(a2+2-6)2+(a3+2-6)2]
=![]() [(a1-4)2+(a2-4)2+(a3-4)2]
[(a1-4)2+(a2-4)2+(a3-4)2]
=3.
故选:B.
-
科目: 来源: 题型:
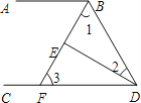
查看答案和解析>>【题目】如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠3的度数.
-
科目: 来源: 题型:
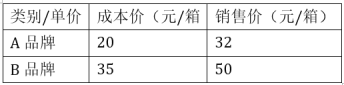
查看答案和解析>>【题目】列二元一次方程组解应用题:某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
(1)该大型超市购进A、B品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
-
科目: 来源: 题型:
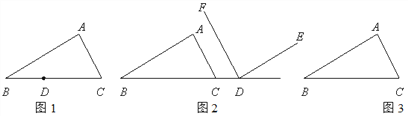
查看答案和解析>>【题目】已知:△ABC和同一平面内的点D.
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
① 依题意,在图1中补全图形;
② 判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份
4月
5月
6月
用水量
15
17
21
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,对四边形ABCD是平行四边形的下列判断,正确的打“√”,错误的打“×”.
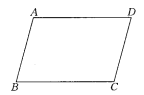
(1)因为AD∥BC,AB=CD,所以ABCD是平行四边形.(____)
(2)因为AB∥CD,AD=BC,所以ABCD是平行四边形.(____)
(3)因为AD∥BC,AD=BC,所以ABCD是平行四边形.(____)
(4)因为AB∥CD,AD∥BC,所以ABCD是平行四边形.(____)
(5)因为AB=CD,AD=BC,所以ABCD是平行四边形.(____)
(6)因为AD=CD,AB=AC,所以ABCD是平行四边形.(____)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2,x3,x2019都是不等于0的有理数,若
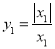 ,求y1的值.
,求y1的值. 当x1>0时,
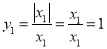 ;当x1<0时,
;当x1<0时,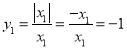 ,所以y1=±1,值有两个.
,所以y1=±1,值有两个.(1)若
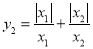 ,求y2的值为 ;
,求y2的值为 ;(2)若
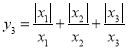 ,则y3的值为 ;
,则y3的值为 ;(3)由以上探究猜想,
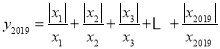 共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
相关试题

