【题目】如图所示,对四边形ABCD是平行四边形的下列判断,正确的打“√”,错误的打“×”.
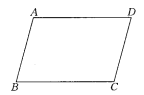
(1)因为AD∥BC,AB=CD,所以ABCD是平行四边形.(____)
(2)因为AB∥CD,AD=BC,所以ABCD是平行四边形.(____)
(3)因为AD∥BC,AD=BC,所以ABCD是平行四边形.(____)
(4)因为AB∥CD,AD∥BC,所以ABCD是平行四边形.(____)
(5)因为AB=CD,AD=BC,所以ABCD是平行四边形.(____)
(6)因为AD=CD,AB=AC,所以ABCD是平行四边形.(____)
参考答案:
【答案】× × ∨ ∨ ∨ ×
【解析】
平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.根据判定定理判断即可.
解:(1)(2)中的四边形可能是等腰梯形,不能判定是平行四边形,故错误;
(3)(4)(5)是平行四边形的判定定理,可判定是平行四边形,故正确;
(6)不符合平行四边形的判定定理,不能判定是平行四边形,故错误;
故答案为:(1).×;(2).×;(3).∨;(4).∨;(5).∨;(6).×.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC和同一平面内的点D.
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
① 依题意,在图1中补全图形;
② 判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
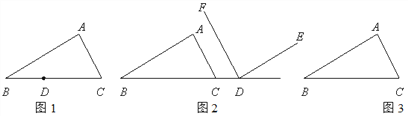
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据
 ,
, ,
,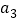 的平均数为4,方差为3,那么数据
的平均数为4,方差为3,那么数据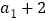 ,
, ,
,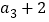 的平均数和方差分别是( )
的平均数和方差分别是( )A. 4, 3 B. 6
 3 C. 3
3 C. 3 4 D. 6
4 D. 6 5
5 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份
4月
5月
6月
用水量
15
17
21
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2,x3,x2019都是不等于0的有理数,若
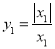 ,求y1的值.
,求y1的值. 当x1>0时,
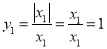 ;当x1<0时,
;当x1<0时,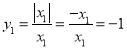 ,所以y1=±1,值有两个.
,所以y1=±1,值有两个.(1)若
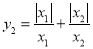 ,求y2的值为 ;
,求y2的值为 ;(2)若
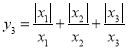 ,则y3的值为 ;
,则y3的值为 ;(3)由以上探究猜想,
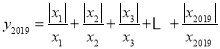 共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 .
共有 个不同的值,在y2019这些不同的值中,最大的值和最小的值的差等于 . -
科目: 来源: 题型:
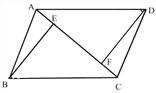
查看答案和解析>>【题目】如图,已知在四边形ABCD中,AB=CD,BC=AD,E、F是对角线AC上两点,且AE=CF.求证:BE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )

A. ①③B. ①②④C. ①③④D. ①②③④
相关试题

