【题目】已知:△ABC和同一平面内的点D.
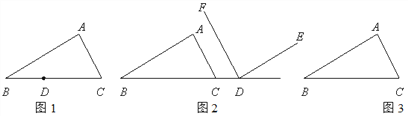
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
① 依题意,在图1中补全图形;
② 判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
参考答案:
【答案】(1)① 补全图形见解析;② ∠EDF=∠A;
(2)DE∥BA,证明见解析;
(3)∠EDF=∠A,∠EDF+∠A=180°
【解析】试题分析:(1)①依题意补全图形即可;②由平行四边形的判定可得四边形AEDF是平行四边形,再由平行四边形对角相等得结果;(2)延长BA,由平行线的性质得∠2=∠3,等量代换得∠1=∠3,由内错角相等两直线平行得DE∥BA;(3)分情况讨论即可.
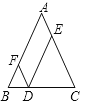
试题解析:(1)① 补全图形如下:
 ;
;
② ∠EDF=∠A.
∵DE∥BA,DF∥CA
∴四边形AEDF是平行四边形
∴∠EDF=∠A
(2)DE∥BA.
证明:如图,延长BA交DF与G.
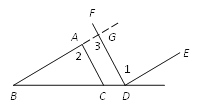
∵ DF∥CA,
∴ ∠2=∠3.
又∵ ∠1=∠2,
∴ ∠1=∠3.
∴ DE∥BA
(3)由(2)知∠EDF=∠A,
当动点D如下位置时,
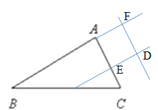
∵四边形AEDF是平行四边形,
∴∠BAC=∠AFD, ∠AFD+∠EDF=180°,
∴∠EDF+∠BAC=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】合并同类项解方程:一般是把方程左边含未知数的项合并,把右边的常数项合并,从而把方程化简为________(a≠0,a、b是常数)的形式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车生产商新推出一款新型电动低能耗汽车,由于该型号汽车经济适用性强,销量快速增长,1月份该型号汽车的销量为2000辆,3月份该型号汽车的销量达4500辆.设该型号汽车销量的月平均增长率为x,则根据题意可列方程为( )
A. 2000(1+x)2=4500 B. 2000(1+2x)=4500
C. 2000(1-x)2 =4500 D. 2000x2=4500
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人进行射击测试,每人10次射击成绩的平均值都是8.9环,方差分别是S甲2=0.53,S乙2=0.51,S丙2=0.43,则三人中成绩最稳定的是______(填“甲”或“乙”或“丙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,AC=BC=2,D是边AB上一动点(A、B两点除外),将△CAD绕点C按逆时针方向旋转角α得到△CEF,其中点E是点A的对应点,点F是点D的对应点.
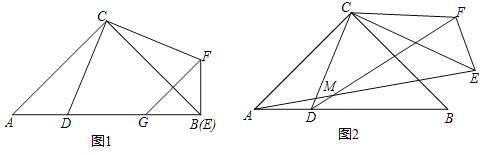
(1)如图1,当α=90°时,G是边AB上一点,且BG=AD,连接GF.求证:GF∥AC;
(2)如图2,当90°≤α≤180°时,AE与DF相交于点M.
①当点M与点C、D不重合时,连接CM,求∠CMD的度数;
②设D为边AB的中点,当α从90°变化到180°时,求点M运动的路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
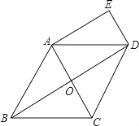
(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有关“总量=________”的实际问题:解决这类问题一般是先设其中一部分量为x,再用x表示其他各部分量,然后根据等量关系列出方程即可.
相关试题

