【题目】随着科技进步,无人机的应用越来越广,如图1,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部C的俯角.

(1)如果上述仰角与俯角分别为30°与60°,且该楼的高度为30米,求该时刻无人机的竖直高度CD;
(2)如图2,如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)过A作AD⊥CB,垂足为点D.在Rt△ABD中,∠BAD=30°.得AB=2BD;在Rt△ABC中,∠CBA=60°,得ACB=30°故BC=2AB , 故CD=BC-BD
(2)设CD=x,则 BD=m-x ,tanα=![]() =
=![]() ;tanβ=
;tanβ=![]() =
=![]() ,所以
,所以 ,
,
tanβ·(m-x)=tanα·x,可求x.
(1)解 :过A作AD⊥CB,垂足为点D.
∵在Rt△ABD中,∠BAD=30°,
∴AB=2BD
∵在Rt△ABC中,∠CBA=60°,
∴∠ACB=30°
∴BC=2AB ,又∵BC=30米 ,
∴AB=15米
∴BD=7.5米
∴CD=BC-BD=30-7.5=22.5米
答:无人机的竖直高度CD为22.5米。
(2)解 :设CD=x,则 BD=m-x ,
在Rt△ABD中,∠BAD=α,
∴tanα=![]() =
=![]() ;
;
在Rt△ADC中,∠DCA=β ,
∴tanβ=![]() =
=![]() ,
,
∴ ,
,
tanβ·(m-x)=tanα·x
∴x=![]()
-
科目: 来源: 题型:
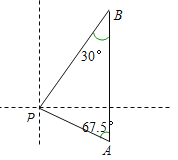
查看答案和解析>>【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的周长是12,D是AC边上的中点,点E在BC边的延长线上,如果DE=DB,那么CE的长是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=
 , AD=4.
, AD=4.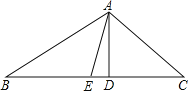
(1)求BC的长;
(2)求tan∠DAE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度
1:20
1:16
1:12
最大高度(米)
1.50
1.00
0.75
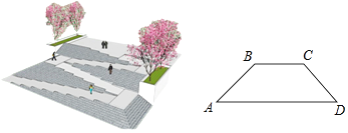
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(一)阅读
求x+6x+11的最小值.
解:x+6x+11
=x2+6x+9+2
=(x+3)2+2
由于(x+3)2的值必定为非负数,所以(x+3)2+2,即x2+6x+11的最小值为2.

(二)解决问题
(1)若m2+2mn+2n2-6n+9=0,求(
 )-3的值;
)-3的值;(2)对于多项式x2+y-2x+2y+5,当x,y取何值时有最小值,最小值为多少?
相关试题

