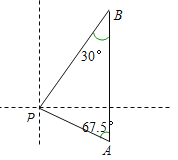
【题目】马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
参考答案:
【答案】向阳号轮船所处位置B与城市P的距离为100海里.
【解析】试题分析: 首先根据题意可得PC⊥AB,然后设PC=x海里,分别在Rt△APC中与Rt△PCB中,利用正切函数求得出AC与BC的长,由AB=21×5,即可得方程,解此方程即可求得x的值,继而求得答案.
试题解析:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=![]() ,
,
∴AC=![]() .
.
在Rt△PCB中,∵tan∠B=![]() ,
,
∴BC=![]() .
.
∵AC+BC=AB=21×5,
∴![]() ,
,
解得![]() .
.
∵![]() ,
,
∴![]() (海里).
(海里).
∴向阳号轮船所处位置B与城市P的距离为100海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,OA⊥OB,∠BOC=50°,且∠AOD:∠COD=4:7.画出∠BOC的角平分线OE,并求出∠DOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2-x-1与x轴的一个交点的坐标为(m,0),则代数式m2-m+2019的值为( )
A. 2015B. 2016C. 2019D. 2020
-
科目: 来源: 题型:
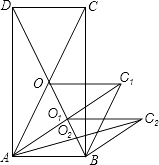
查看答案和解析>>【题目】如图所示,矩形ABCD的面积为128cm2 , 它的两条对角线交于点O1 , 以AB、AO1为两边邻作平行四边形ABC1O1 , 平行四边形ABC1O1的对角线交于点O2 , 同样以AB、AO2为两邻边作平行四边形ABC2O2 , …,依此类推,则平行四边形ABC7O7的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】能断定A,B,C三点共线的是( )
A. AB=6,AC=2,BC=5B. AB=6,AC=2,BC=4
C. AB=6,AC=3,BC=4D. AB=6,AC=5,BC=4
-
科目: 来源: 题型:
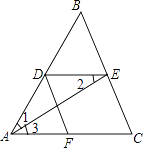
查看答案和解析>>【题目】在△ABC中,AE平分∠BAC交BC于E,DE∥AC交AB于D,过D作DF∥BC交AC于F,若AD=3,求FC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪和小敏在研究绝对值的问题时,遇到了这样一道题:
(1)当式子|x﹣1|+|x+5|取最小值时,x应满足的条件是 , 此时的最小值是 . 小聪说:利用数轴求线段的长可以解决这个问题.如图,点A,B对应的数分别为﹣5,1,则线段AB的长为6,我发现也可通过|1﹣(﹣5)|或|﹣5﹣1|来求线段AB的长,即数轴上两点间的线段的长等于它们所对应的两数差的绝对值.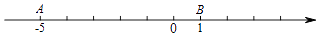
小敏说:我明白了,若点C在数轴上对应的数为x,线段AC的长就可表示为|x﹣(﹣5)|,那么|x﹣1|表示的是线段的长.
小聪说:对,求式子|x﹣1|+|x+5|的最小值就转化为数轴上求线段AC+BC长的最小值,而点C在线段AB上时AC+BC=AB最小,最小值为6.
小敏说:点C在线段AB上,即x取﹣5,1之间的有理数(包括﹣5,1),因此相应x的取值范围可表示为﹣5≤x≤1时,最小值为6.
请你根据他们的方法解决下面的问题:
(2)小敏说的|x﹣1|表示的是线段的长;
(3)当式子|x﹣3|+|x+2|取最小值时,x应满足的条件是;
(4)当式子|x﹣2|+|x+3|+|x+4|取最小值时,x应满足的条件是;
(5)当式子|x﹣a|+|x﹣b|+|x﹣c|+|x﹣d|(a<b<c<d)取最小值时,x应满足的条件是 , 此时的最小值是 .
相关试题

