【题目】把多边形的某些边向两方延长,其他各边若不全在延长所得直线的同侧,则把这样的多边形叫做凹多边形.如图①五边形![]() 中,作直线
中,作直线![]() ,则边
,则边![]() 、
、![]() 分别在直线
分别在直线![]() 的两侧,所以五边形
的两侧,所以五边形![]() 就是一个凹五边形.我们简单研究凹多边形的边和角的性质.
就是一个凹五边形.我们简单研究凹多边形的边和角的性质.

(1)如图②,在凹六边形![]() 中,探索
中,探索![]() 与
与![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、之间的关系;
、之间的关系;
(2)如图③,在凹四边形![]() 中,证明
中,证明![]() .
.
参考答案:
【答案】(1)∠BCD=∠A+∠F+∠E+∠ABC+∠EDC-360°;(2)证明见解析.
【解析】试题分析: (1)根据题意结合凸多边形的性质得出540°-(180°-∠BCD)=∠A+∠B+∠D+∠E+∠F,进而得出答案;
(2)利用三角形三边关系,再结合不等式的性质进而得出答案.
试题解析:
(1)连接BD
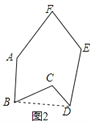
在△BCD中,
∠BCD+∠CBD+∠CDB=180°
又在五边形ABDEF中,
∠A+∠F+∠E+∠ABC+∠EDC+∠CBD+∠CDB=540°
两式相减得
∠BCD=∠A+∠F+∠E+∠ABC+∠EDC-360°
(2)延长BC交AD于点E,
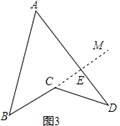
∴AB+AD=AB+AE+ED
在△ABE中 AB+AE>BE
∴AB+AD>BE+ED
又∵BE=BC+CE
在△ECD中,CE+ED>CD
∴BE+ED>BC+CD
∴AB+AD>BC+CD
点睛:此题主要考查了四边形综合以及凸多边形的性质以及凹多边形与凸多边形的性质等知识,正确将凹多边形与凸多边形的关系是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解答问题:
我们知道
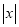 的几何意义是在数轴上数
的几何意义是在数轴上数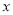 对应的点与原点的距离:
对应的点与原点的距离: 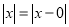 ,也就是说,
,也就是说, 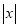 表示在数轴上数
表示在数轴上数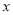 与数0对应点之间的距离;
与数0对应点之间的距离;这个结论可以推广为
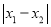 表示在数轴上数
表示在数轴上数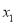 和数
和数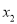 对应的点之间的距离;
对应的点之间的距离;例1解方程
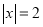 ,容易看出,在数轴上与原点距离为2的点对应的数为
,容易看出,在数轴上与原点距离为2的点对应的数为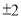 ,即该方程的解为
,即该方程的解为 .
.例2解不等式
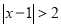 ,如图,在数轴上找出
,如图,在数轴上找出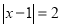 的解,即到1的距离为2的点对应的数为
的解,即到1的距离为2的点对应的数为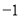 ,3,则
,3,则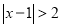 的解集为
的解集为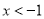 或
或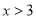 .
.
例3解方程
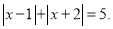 由绝对值的几何意义知,该方程表示求在数轴上与1和
由绝对值的几何意义知,该方程表示求在数轴上与1和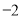 的距离之和为5的对应的
的距离之和为5的对应的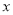 的值.在数轴上,1和
的值.在数轴上,1和 的距离为3,满足方程的
的距离为3,满足方程的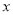 对应的点在1的右边或
对应的点在1的右边或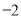 的左边,若
的左边,若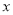 对应的点在1的右边,由下图可以看出
对应的点在1的右边,由下图可以看出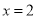 ;同理,若
;同理,若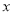 对应的点在
对应的点在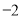 的左边,可得
的左边,可得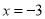 ,故原方程的解是
,故原方程的解是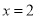 或
或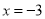 .
.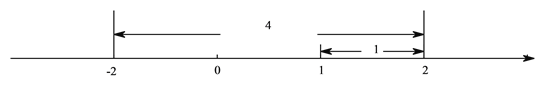
回答问题:(只需直接写出答案)
①解方程

②解不等式
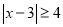
③解方程
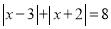
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
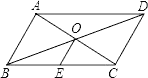
A. OE=
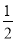 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
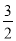 ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.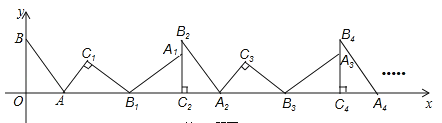
-
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺1∶8000000的地图上,量得太原到北京的距离为6.4厘米,则太原到北京的实际距离为 公里。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在任意三角形、锐角、长方形三种图形中,有且只有一条对称轴的是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )
A. 16 B. 12 C. 16或12 D. 24
相关试题

